Bài 1 trang 62 SGK Hình học 10

Đề bài

Hãy nhắc lại định nghĩa giá trị lượng giác của một  góc $α$ với $0^0≤  α ≤ 180^0$. Tại sao khi $α$ là một góc nhọn thì giá trị lượng giác này lại chính là các tỉ số lượng giác đã được học ở lớp 9?

Lời giải chi tiết

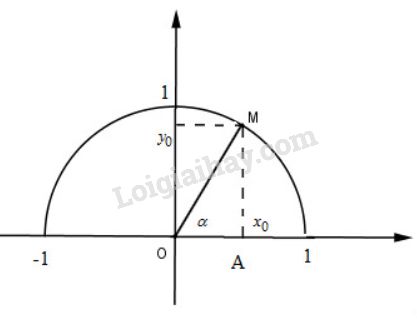
+) Định nghĩa: Với mỗi góc $α$ $(0^0≤  α ≤ 180^0)$ ta xác định một điểm $M$ trên nửa đường tròn đơn vị sao cho $\widehat {xOM} =  α$ và giả sử điểm $M$ có tọa độ $M (x_0;y_0)$.

Khi đó ta có định nghĩa:

$\sin α = y_0$

$\cos α = x_0$

$\tan α =  {{{y_0}} \over {{x_0}}}$

$\cot α =  {{{x_0}} \over {{y_0}}}$

Các số $\sin α, \cos α, \tan α, \cot α$ được gọi là các giá trị lượng giác của góc $α$.

+) Khi $α$ là các góc nhọn thì:

Trong tam giác $OAM$ vuông tại $A$, ta có:

$\sin \alpha   = \frac{{MA}}{{OM}}={{{y_0}} \over 1} = {y_0}$

$\cos \alpha  = {{OA} \over {OM}} = {{{x_0}} \over 1} = {x_0}$

$\tan \alpha  = {{AM} \over {OA}} = {{{y_0}} \over {{x_0}}}$

$\cot \alpha  = {{OA} \over {AM}} = {{{x_0}} \over {{y_0}}}$

HocTot.Nam.Name.Vn