Các câu hỏi trắc nghiệm ôn tập chương III trang 122 SGK Hình học 11 Nâng cao

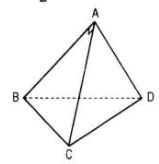
LG 1

Cho tứ diện ABCD có trọng tâm G. Mệnh đề nào sau đây là sai ?

A. \(\overrightarrow {OG}  = {1 \over 4}\left( {\overrightarrow {OA}  + \overrightarrow {OB}  + \overrightarrow {OC}  + \overrightarrow {OD} } \right)\)

B. \(\overrightarrow {GA}  + \overrightarrow {GB}  + \overrightarrow {GC}  + \overrightarrow {GD}  = \overrightarrow 0 \)

C. \(\overrightarrow {AG}  = {2 \over 3}\left( {\overrightarrow {AB}  + \overrightarrow {AC}  + \overrightarrow {AD} } \right)\)

D. \(\overrightarrow {AG}  = {1 \over 4}\left( {\overrightarrow {AB}  + \overrightarrow {AC}  + \overrightarrow {AD} } \right)\)

Giải chi tiết:

(A), (B) đúng.

Gọi G₁ là trọng tâm ΔBCD ta có \(\overrightarrow {AG}  = {3 \over 4}\overrightarrow {A{G_1}}  = {1 \over 4}\left( {\overrightarrow {AB}  + \overrightarrow {AC}  + \overrightarrow {AD} } \right)\) nên (D) đúng.

Vậy chọn (C)

LG 2

Mệnh đề nào sau đây là đúng ?

A. Hai đường thẳng cùng vuông góc với một đường thẳng thì song song với nhau ;

B. Hai đường thẳng cùng vuông góc với một đường thẳng thì vuông góc với nhau ;

C. Một đường thẳng vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng kia ;

D. Một đường thẳng vuông góc với một trong hai đường thẳng vuông góc với nhau thì song song với đường thẳng còn lại.

Giải chi tiết:

Chọn (C)

LG 3

Cho hai đường thẳng phân biệt a, b và mặt phẳng (P), trong đó a ⊥ (P). Mệnh đề nào sau đây là sai ?

A. Nếu b // (P) thì b ⊥ a

B. Nếu b ⊥ (P) thì b // a

C. Nếu b // a thì b ⊥ (P)

D. Nếu b ⊥ a thì b // (P)

Giải chi tiết:

Nếu b ⊥ a thì có thể b ⊂ (P)

Chọn (D)

LG 4

Tìm mệnh đề đúng trong các mệnh đề sau :

A. Hai đường thẳng cùng vuông góc với một đường thẳng thì song song ;

B. Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thì song song ;

C. Hai mặt phẳng phân biệt cùng vuông góc với một đường thẳng thì song song ;

D. Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thì song song.

Giải chi tiết:

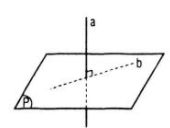
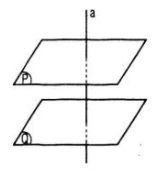
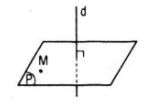
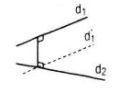
\(\left\{ {\matrix{   {(P) \ne (Q)}  \cr   {(P) \bot a}  \cr   {(Q) \bot a}  \cr } } \right. \Rightarrow (P)//(Q)\)

Chọn (C)

LG 5

Mệnh đề nào sau đây là đúng ?

A. Hai đường thẳng vuông góc với nhau thì mọi đường thẳng nằm trong mặt phẳng này sẽ vuông góc với mặt phẳng kia ;

B. Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thì vuông góc với nhau ;

C. Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau ;

D. Ba mệnh đề trên đều sai.

Giải chi tiết:

Chọn D.

(A). Sai theo hình vẽ bên

\(\left\{ {\matrix{   {(P) \bot (Q)}  \cr   {a \subset (Q)}  \cr } } \right.\) nhưng a // (P)

(B), (C) sai theo hình vẽ sau.

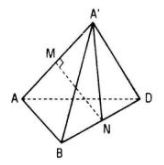
LG 6

Trong các mệnh đề sau, mệnh đề nào đúng ?

A. Có duy nhất một đường thẳng đi qua một điểm cho trước và vuông góc với một đường thẳng cho trước ;

B. Có duy nhất một mặt phẳng đi qua một đường thẳng cho trước và vuông góc với một mặt phẳng cho trước ;

C. Có duy nhất một mặt phẳng đi qua một điểm cho trước và vuông góc với một mặt phẳng cho trước ;

D. Có duy nhất một mặt phẳng đi qua một điểm cho trước và vuông góc với một đường thẳng cho trước.

Giải chi tiết:

Chọn (D)

LG 7

Tìm mệnh đề đúng trong các mệnh đề sau :

A. Nếu hình hộp có hai mặt là hình chữ nhật thì nó là hình hộp chữ nhật ;

B. Nếu hình hộp có ba mặt là hình chữ nhật thì nó là hình hộp chữ nhật ;

C. Nếu hình hộp có bốn mặt là hình chữ nhật thì nó là hình hộp chữ nhật ;

D. Nếu hình hộp có năm mặt là hình chữ nhật thì nó là hình hộp chữ nhật.

Giải chi tiết:

Chọn (D)

LG 8

Trong các mệnh đề sau, mệnh đề nào đúng ?

A. Nếu hình hộp có hai mặt là hình vuông thì nó là hình lập phương ;

B. Nếu hình hộp có ba mặt chung một đỉnh là hình vuông thì nó là hình lập phương ;

C. Nếu hình hộp có sáu mặt bằng nhau thì nó là hình lập phương ;

D. Nếu hình hộp có bốn đường chéo bằng nhau thì nó là hình lập phương .

Giải chi tiết:

Chọn (B)

LG 9

Cho hình chóp S.ABC có đáy là tam giác đều. Tìm mệnh đề đúng trong các mệnh đề sau :

A. S.ABC là hình chóp đều nếu các mặt bên của nó là tam giác cân ;

B. S.ABC là hình chóp đều nếu các mặt bên của nó là tam giác cân với đỉnh S ;

C. S.ABC là hình chóp đều nếu góc giữa các mặt phẳng chứa các mặt bên và mặt phẳng chứa đáy bằng nhau ;

D. S.ABC là hình chóp đều nếu các mặt bên có diện tích bằng nhau.

Giải chi tiết:

Chọn (B)

LG 10

Tìm mệnh đề đúng trong các mệnh đề sau :

A. Đường vuông góc chung của hai đường thẳng chéo nhau thì nằm trong mặt phẳng chứa đường thẳng này và vuông góc với đường thẳng kia ;

B. Đường vuông góc chung của hai đường thẳng chéo nhau thì vuông góc với mặt phẳng chứa đường thẳng này và song song với đường thẳng kia ;

C. Một đường thẳng là đường vuông góc chung của hai đường thẳng chéo nhau nếu nó vuông góc với cả hai đường thẳng đó ;

D. Các mệnh đề trên đều sai.

Giải chi tiết:

Chọn (B)

LG 11

Hình tứ diện ABCD có AB, AC, AD đôi một vuông góc là AB = AC = AD = 3.

Diện tích tam giác BCD bằng

A. \({{9\sqrt 3 } \over 2}\)

B. \({{9\sqrt 2 } \over 3}\)

C. 27

D. \({{27} \over 2}\)

Giải chi tiết:

Chọn (A).

Ta có: BC = CD = BD = \(3\sqrt 2 \)

Tam giác BCD đều cạnh \(a = 3\sqrt 2 \) nên

\({S_{BCD}} = {{{a^2}\sqrt 3 } \over 4} = {{18\sqrt 3 } \over 4} = {{9\sqrt 3 } \over 2}\)

LG 12

Hình hộp ABCD.A’B’C’D’ có AB = AA’ = AD = a và \(\widehat {A'AB} = \widehat {A'AD} = \widehat {BAD} = 60^\circ .\) Khi đó, khoảng cách giữa các đường thẳng chứa các cạnh đối diện của tứ diện AA’BD bằng :

A. \({{a\sqrt 2 } \over 2}\)

B. \({{a\sqrt 3 } \over 2}\)

C. \(a\sqrt 2 \)

D. \({{3a} \over 2}\)

Giải chi tiết:

Chọn (A)

Tứ diện A’ABD là tứ diện đều cạnh a.

M, N lần lượt là trung điểm AA’, BD.

MN là đoạn vuông góc chung của AA’ và BD. Ta có:

\(M{N^2} = A'{N^2} - A'{M^2}\)

            \(= {\left( {{{a\sqrt 3 } \over 2}} \right)^2} - {\left( {{a \over 2}} \right)^2}\)

            \(= {{3{a^2}} \over 4} - {{{a^2}} \over 4} = {{{a^2}} \over 2} \)

\(\Rightarrow {\rm M}{\rm N} = {{a\sqrt 2 } \over 2}\)

HocTot.Nam.Name.Vn