Bài tập cuối tuần Toán 5 tuần 8 - Đề 2 ( Có đáp án và lời giải chi tiết)Tải vềBài tập cuối tuần 8 - Đề 2 bao gồm các bài tập chọn lọc với các dạng bài tập giúp các em ôn lại kiến thức đã học trong tuần Đề bài Bài 1: Khoanh vào chữ cái đặt trước câu trả lời đúng: Viết số thập phân 750,05000 dưới dạng gọn nhất. A. 75,5 B. 7,55 C. 750,5 D. 750,05 Bài 2: Đúng ghi Đ, sai ghi S: Tìm chữ số \(x\), biết \(\overline {9,58x1} > 9,5871\) A. \(x\) = 6 C. \(x\) = 8 Bài 3: Đúng ghi Đ, sai ghi S: a) \(\dfrac{7}{{10}} < 0,7\) b) \(\dfrac{7}{{10}} = 0,7\) c) \(\dfrac{{1232}}{{1000}} = 1,232\) d) \(\dfrac{{1232}}{{1000}} > 1,232\) e) \(5\dfrac{{21}}{{1000}} < 5,21\) f) \(5\dfrac{{21}}{{1000}} > 5,21\) Bài 4: Đúng ghi Đ, sai ghi S: Các số sau đây được sắp xếp theo thứ tự từ bé đến lớn là: a) 0,51; 0,051; 0,015; 0,15; 0,105; 0,501 b) 0,015; 0,051; 0,105; 0,15; 0,501; 0,51 Bài 5: Điền dấu (>, =, <) vào chỗ chấm: a) 58,788 … 58,79 b) 0,128 … 0,13 c) 19,16 … 19,155 d) 224,02000 … 224,02 Bài 6: Tìm số thập phân \(x\), biết:
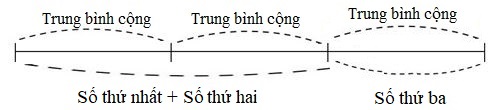
Bài 7: Viết đáp án dưới dạng số thập phân: Trung bình cộng của ba số là \(\dfrac{7}{8}\). Số thứ ba bằng trung bình cộng của số thứ nhất và số thứ hai. Số thứ nhất hơn số thứ hai là \(\dfrac{1}{5}\). Tìm ba số đó. ........................................................................................................................................ ........................................................................................................................................ ........................................................................................................................................ ........................................................................................................................................ ........................................................................................................................................ ........................................................................................................................................ Lời giải chi tiết Bài 1: Phương pháp giải: Nếu một số thập phân có chữ số 0 ở tận cùng bên phải phần thập phân thì khi bỏ chữ số 0 đó đi, ta được số mới bằng số ban đầu. Cách giải: Ta có: 750,05000 = 750,0500 = 750,050 = 750,05. Vậy số thập phân 750,05000 viết dưới dạng gọn nhất là 750,05. Đáp án đúng là D. Bài 2: Phương pháp giải: Ở đây hai số thập phân có phần nguyên, hàng phần mười, phần trăm giống nhau nên ta sẽ đi so sánh hàng phần nghìn, số thập phân nào có hàng phần nghìn lớn hơn thì lớn hơn. Cách giải: Hai số thập phân đã cho có phần nguyên, hàng phần mười, phần trăm giống nhau. Theo đề bài, \(\overline {9,58x1} > 9,5871\), do đó \(x = 8\) hoặc \(x = 9\). Vậy nên ta có kết quả: A. \(x\) = 6 C. \(x\) = 8 Bài 3: Phương pháp giải: Ta thực hiện đưa phân số về dạng số thập phân rồi so sánh kết quả vừa tìm được với số thập phân cho ở đề bài. Cách giải: Ta có: \(\dfrac{7}{{10}} = 0,7\); \(\dfrac{{1232}}{{1000}} = 1,232\); \(5\dfrac{{21}}{{1000}} = 5,021 < 5,21\). Vậy nên ta có kết quả: a) \(\dfrac{7}{{10}} < 0,7\) b) \(\dfrac{7}{{10}} = 0,7\) c) \(\dfrac{{1232}}{{1000}} = 1,232\) d) \(\dfrac{{1232}}{{1000}} > 1,232\) e) \(5\dfrac{{21}}{{1000}} < 5,21\) f) \(5\dfrac{{21}}{{1000}} > 5,21\) Bài 4: Phương pháp giải: Để so sánh hai số thập phân có cùng phần nguyên, ta so sánh phần thập phân, lần lượt từ hàng phần mười, phần trăm, phần nghìn,… đến cùng một hàng nào đó, số thập phân nào có chữ số ở hàng tương ứng lớn hơn thì số đó lớn hơn. Cách giải: So sánh các số ta có: 0,015 < 0,051 < 0,105 < 0,15 < 0,501 < 0,51. Do đó, các số được sắp xếp theo thứ tự từ bé đến lớn là: 0,015; 0,051; 0,105; 0,15; 0,501; 0,51. Vậy ta có kết quả: a) 0,51; 0,051; 0,015; 0,15; 0,105; 0,501 b) 0,015; 0,051; 0,105; 0,15; 0,501; 0,51 Bài 5: Phương pháp giải: - Để so sánh hai số thập phân có cùng phần nguyên, ta so sánh phần thập phân, lần lượt từ hàng phần mười, phần trăm, phần nghìn,… đến cùng một hàng nào đó, số thập phân nào có chữ số ở hàng tương ứng lớn hơn thì số đó lớn hơn. - Nếu một số thập phân có chữ số 0 ở tận cùng bên phải phần thập phân thì khi bỏ chữ số 0 đó đi, ta được số mới bằng số ban đầu. Cách giải: a) 58,788 < 58,79 b) 0,128 < 0,13 c) 19,16 > 19,155 d) 224,02000 = 224,02 Bài 6: Phương pháp giải: Thực hiện giải bài toán tìm \(x\) như thông thường, ta giải ra kết quả là phân số rồi quy đổi sang số thập phân. Cách giải: a) \(x + \dfrac{5}{8} = \dfrac{{11}}{5}\) \(\begin{array}{l}x = \dfrac{{11}}{5} - \dfrac{5}{8}\\x = \dfrac{{63}}{{40}}\\x = \dfrac{{1575}}{{1000}} = 1,575\end{array}\) b) \(x - \dfrac{5}{2} = \dfrac{1}{{25}}\) \(\begin{array}{l}x = \dfrac{1}{{25}} + \dfrac{5}{2}\\x = \dfrac{{127}}{{50}}\\x = \dfrac{{254}}{{100}} = 2,54\end{array}\) c) \(x \times \dfrac{2}{{11}} = \dfrac{1}{5}\) \(\begin{array}{l}x = \dfrac{1}{5}:\dfrac{2}{{11}}\\x = \dfrac{{11}}{{10}}\\x = 1,1\end{array}\) d) \(x:\dfrac{8}{5} = \dfrac{{13}}{{16}}\) \(\begin{array}{l}x = \dfrac{{13}}{{16}} \times \dfrac{8}{5}\\x = \dfrac{{13}}{{10}}\\x = 1,3\end{array}\) Bài 7: Phương pháp giải: Số thứ ba bằng trung bình cộng của số thứ nhất và số thứ hai nên số thứ ba bằng trung bình cộng của cả ba số. - Số thứ ba = trung bình cộng ba số. - Tổng của số thứ nhất và số thứ hai = số thứ ba × 2. - Tìm số thứ hai theo bài toán tìm hai số khi biết tổng và hiệu của hai số: Số thứ hai = ( Tổng – Hiệu) : 2. - Số thứ nhất = tổng của số thứ nhất và thứ hai – số thứ hai. Cách giải: Ta có sơ đồ:
Số thứ ba bằng trung bình cộng của số thứ nhất và số thứ hai nên trung bình cộng của cả ba số bằng số thứ ba. Mà: \(\dfrac{7}{8} = \dfrac{{875}}{{1000}}\)= 0,875. Vậy số thứ ba bằng 0,875. Tổng của số thứ nhất và thứ hai là: \(\dfrac{7}{8} \times 2 = \dfrac{7}{4}\) Số thứ hai là: \(\left( {\dfrac{7}{4} - \dfrac{1}{5}} \right):2 = \dfrac{{31}}{{40}} = \dfrac{{775}}{{1000}} = 0,775\) Số thứ nhất là: \(\dfrac{7}{4} - \dfrac{{31}}{{40}} = \dfrac{{39}}{{40}} = \dfrac{{975}}{{1000}} = 0,975\) Đáp số: Số thứ nhất: 0,975 ; Số thứ hai: 0,775 ; Số thứ ba: 0,875. HocTot.Nam.Name.Vn
|