Đề bài

Cho hai đường tròn $\left( O \right)$ và $\left( {O'} \right)$tiếp xúc ngoài tại $A$. Kẻ các đường kính $AOB;AO'C$. Gọi $DE$ là tiếp tuyến chung của hai đường tròn $\left( {D \in \left( O \right);E \in \left( {O'} \right)} \right)$. Gọi $M$ là giao điểm của $BD$ và $CE$. Tính diện tích tứ giác $ADME$ biết $\widehat {DOA} = 60^\circ $ và $OA = 8\,cm$

A.

$12\sqrt 3 \,\,c{m^2}$
B.

$ \dfrac{64}{3}\sqrt 3 \,\,c{m^2}$
C.

$ \dfrac{32}{3}\sqrt 3 \,\,c{m^2}$
D.

$36\,\,c{m^2}$

Phương pháp giải

Sử dụng tính chất đường nối tâm của hai đường tròn cắt nhau và hệ thức lượng trong tam giác vuông.

Diện tích hình chữ nhật bằng tích chiều dài và chiều rộng.

Lời giải của GV HocTot.Nam.Name.Vn

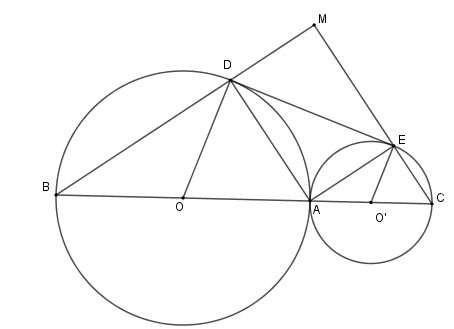
Xét $\left( O \right)$ có $OD = OA \Rightarrow \Delta OAD$ cân tại $O \Rightarrow \widehat {ODA} = \widehat {OAD}$

Xét $\left( {O'} \right)$ có $O'E = O'A \Rightarrow \Delta O'EB$ cân tại $O' \Rightarrow \widehat {O'EA} = \widehat {O'AE}$

Mà $\widehat O + \widehat {O'} = 360^\circ - \widehat {O'ED} - \widehat {ODE} = 180^\circ $

$ \Leftrightarrow 180^\circ - \widehat {ODA} - \widehat {OAD} + 180^\circ - \widehat {O'EA} - \widehat {O'AE} = 180^\circ \Leftrightarrow 2\left( {\widehat {OAD} + \widehat {O'AE}} \right) = 180^\circ $

$ \Rightarrow \widehat {OAD} + \widehat {O'AE} = 90^\circ $$ \Rightarrow \widehat {DAE} = 90^\circ \Rightarrow \Delta ADE$ vuông tại $A$.

Mà $\widehat {BDA} = 90^\circ $ ( vì tam giác $BAD$ có cạnh $AB$ là đường kính của $\left( O \right)$và $D \in \left( O \right)$ ) nên $BD \bot AD \Rightarrow \widehat {MDA} = 90^\circ $

Tương tự ta có $\widehat {MEA} = 90^\circ $ .

Nên tứ giác $DMEA$ là hình chữ nhật.

Xét tam giác $OAD$ cân tại $O$ có $\widehat {DOA} = 60^\circ $ nên $\Delta DOA$ đều, suy ra $OA = AD = 8\,cm$ và $\widehat {ODA} = 60^\circ $

$ \Rightarrow \widehat {ADE} = 30^\circ $. Xét tam giác $ADE$ ta có $EA = AD.\tan \widehat {EDA} = 8.\tan 30^\circ = \dfrac{8}{3}\sqrt 3 $

${S_{DMEA}} = AD.AE = 8.\dfrac{8}{3}\sqrt 3 = \dfrac{64}{3}\sqrt 3 \,\,c{m^2}$.

Đáp án : B

Báo lỗi - Góp ý

Các bài tập cùng chuyên đề

Bài 1 :

Nếu hai đường tròn tiếp xúc với nhau thì số điểm chung của hai đường tròn là

Xem lời giải >>

Bài 2 :

Cho hai đường tròn $\left( {O;R} \right)$ và $\left( {O';r} \right)$ với $R > r$ cắt nhau tại hai điểm phân biệt và $OO' = d$. Chọn khẳng định đúng?

Xem lời giải >>

Bài 3 :

Cho hai đường tròn $\left( {O;20cm} \right)$ và $\left( {O';15cm} \right)$ cắt nhau tại $A$ và$B$. Tính đoạn nối tâm $OO'$, biết rằng$AB = 24cm$ và $O$ và $O'$ nằm cùng phía đối với $AB$ .

Xem lời giải >>

Bài 4 :

Cho hai đường tròn $\left( {O;8\,cm} \right)$ và $\left( {O';6cm} \right)$ cắt nhau tại $A,B$ sao cho $OA$ là tiếp tuyến của $\left( {O'} \right)$. Độ dài dây $AB$ là

Xem lời giải >>

Bài 5 :

Cho hai đường tròn $\left( O \right)$ và $\left( {O'} \right)$ tiếp xúc ngoài tại $A$. Kẻ các đường kính $AOB;AO'C$. Gọi $DE$ là tiếp tuyến chung của hai đường tròn $\left( {D \in \left( O \right);E \in \left( {O'} \right)} \right)$. Gọi $M$ là giao điểm của $BD$ và $CE$. Tính diện tích tứ giác $ADME$ biết $\widehat {DOA} = 60^\circ $ và $OA = 6\,cm.$

Xem lời giải >>

Bài 6 :

Cho hai đường tròn $\left( O \right);\left( {O'} \right)$ cắt nhau tại $A,B$, trong đó $O' \in \left( O \right)$. Kẻ đường kính $O'OC$ của đường tròn $\left( O \right)$. Chọn khẳng định sai?

Xem lời giải >>

Bài 7 :

Cho đường thẳng xy và đường tròn (O; R) không giao nhau. Gọi M là một điểm di động trên xy. Vẽ đường tròn đường kính OM cắt đường tròn (O) tại A và B. Kẻ $OH \bot xy$ . Chọn câu đúng.

Xem lời giải >>

Bài 8 :

Cho hai đường tròn (O;5) và (O’;5) cắt nhau tại A và B. Biết OO’=8. Độ dài dây cung AB là

Xem lời giải >>

Bài 9 :

Cho đường tròn tâm $O$ bán kính $R = 2cm$ và đường tròn tâm $O'$ bán kính $R' = 3cm.$ Biết $OO' = 6cm.$ Số tiếp tuyến chung của hai đường tròn đã cho là:

Xem lời giải >>

Bài 10 :

Cho hai đường tròn $\left( {I;7cm} \right)$ và $\left( {K;5cm} \right)$. Biết $IK = 2cm$. Quan hệ giữa hai đường tròn là:

Xem lời giải >>