Nội dung Tổng hợp
Cho hai đường tròn (O;5) và (O′;5) cắt nhau tại A và B. Biết OO′=8. Độ dài dây cung AB là
-
A.
6cm
-
B.
7cm
-
C.
5cm
-
D.
8cm
Tính chất tam giác cân
Đinh lí pi-ta-go
Tính chất hai đường tròn cắt nhau
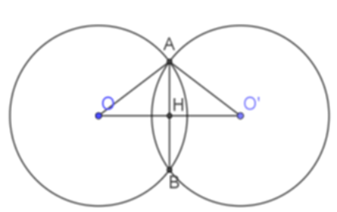
Ta có OA=O′A=5cm nên tam giác AOO′ cân tại A.
Mà AH vuông góc với OO’ nên H là trung điểm của OO’. Suy ra OH=4cm .
Xét tam giác AOH vuông tại H nên suy ra
AH2=OA2−OH2=52−42=9=32.
Vậy AH=3cm .
Mà AB=2AH ( mối quan hệ giữa đường nối tâm và dây cung).
Vậy AB=6cm
Đáp án : A

Các bài tập cùng chuyên đề
Bài 1 :
Cho hai đường tròn (O;R) và (O′;r) với R>r cắt nhau tại hai điểm phân biệt và OO′=d. Chọn khẳng định đúng?
-
A.
d=R−r
-
B.
d>R+r
-
C.
R−r<d<R+r
-
D.
d<R−r
Bài 2 :
Cho hai đường tròn (O;20cm) và (O′;15cm) cắt nhau tại A vàB. Tính đoạn nối tâm OO′, biết rằngAB=24cm và O và O′ nằm cùng phía đối với AB .
-
A.
OO′=7cm
-
B.
OO′=8cm
-
C.
OO′=9cm
-
D.
OO′=25cm
Bài 3 :
Cho hai đường tròn (O);(O′) cắt nhau tại A,B, trong đó O′∈(O). Kẻ đường kính O′OC của đường tròn (O). Chọn khẳng định sai?
-
A.
AC=CB
-
B.
^CBO′=90∘
-
C.
CA,CB là hai tiếp tuyến của (O′)
-
D.
CA,CB là hai cát tuyến của (O′)
Bài 4 :
Cho hai đường tròn (O;4cm) và (O′;3cm) biết OO′=5cm. Hai đường tròn trên cắt nhau tại A và B. Độ dài AB là:
-
A.
2,4cm
-
B.
4,8cm
-
C.
512cm
-
D.
5cm
Bài 5 :
Cho hai đường tròn tiếp xúc ngoài (O;R) và (O′;r) với R>r và OO′=d . Chọn khẳng định đúng?
-
A.
d=R−r
-
B.
d>R+r
-
C.
R−r<d<R+r
-
D.
d=R+r
Bài 6 :
Cho hai đường tròn (O);(O′) cắt nhau tại A,B. Kẻ đường kính AC của đường tròn (O) và đường kính AD của đường tròn (O′). Chọn khẳng định sai?
-
A.
OO′=DC2
-
B.
C,B,D thẳng hàng
-
C.
OO′⊥AB
-
D.
BC=BD
Bài 7 :
Cho hai đường tròn (O;10cm) và (O′;5cm) cắt nhau tại A và B . Tính đoạn nối tâm OO′, biết rằng AB=8cm và O và O′ nằm cùng phía đối với AB . (làm tròn đến chữ số thập phân thứ nhất)
-
A.
OO′≈6,5cm
-
B.
OO′≈6,1cm
-
C.
OO′≈6cm
-
D.
OO′≈6,2cm
Bài 8 :
Cho hai đường tròn (O;5) và (O’;5) cắt nhau tại A và B. Biết OO’=8. Độ dài dây cung AB là
-
A.
6cm
-
B.
7cm
-
C.
5cm
-
D.
8cm
Bài 9 :
Cho hình 5.31, trong đó giả sử O’A < OA.
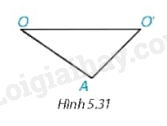
Ta có: OA – O’A < OO’ < OA + O’A. Hãy vẽ hai đường tròn (O; OA) và (O’; O’A) và cho biết hai đường tròn này có mấy điểm chung?
Bài 10 :
Cho đường tròn (O; 5 cm) và điểm I cách O một khoảng 2 cm. Xác định vị trí tương đối của đường tròn đã cho và đường tròn (I; r) trong mỗi trường hợp sau:
a) r = 4 cm;
b) r = 6 cm
Bài 11 :
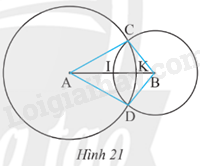
Cho hai đường tròn (A; 6 cm) và (B; 4 cm) cắt nhau tại C, D, AB = 8 cm. Gọi I, K lần lượt là giao điểm của hai đường tròn đã cho với đoạn thẳng AB (Hình 21).
a) Tính độ dài của các đoạn thẳng CA, CB, DA và DB.
b) Điểm I có phải là trung điểm của đoạn thẳng AB không?
c) Tính độ dài của đoạn thẳng IK.
Bài 12 :
Bạn Đan vẽ năm vòng tròn minh họa cho biểu tượng của Thế vận hội Olympic như ở Hình 10. Hình vẽ đó thể hiện những cặp đường tròn cắt nhau. Theo em, hai đường tròn cắt nhau thì chúng có bao nhiêu điểm chung?

Bài 13 :
Cho hai đường tròn (O;14cm),(O′;5cm) với OO′=8cm. Hỏi hai đường tròn đó có cắt nhau hay không?
Bài 14 :
Hai đường tròn (O; 5cm) và (O’; 3cm) cắt nhau. Số giá trị nguyên mà độ dài OO’ có thể nhận được (đơn vị cm) là
-
A.
3.
-
B.
4.
-
C.
5.
-
D.
6.
Bài 15 :
Cho điểm A và đường tròn (O; R) sao cho R<OA<3R.
a) Chứng minh rằng đường tròn (A; 2R) cắt đường tròn (O; R). Gọi B là một trong hai giao điểm của chúng.
b) Gọi C là điểm đối xứng với B qua O. Nối A với C cắt (O) tại D (khác C). Chứng minh rằng AD=DC.
Bài 16 :
Cho tam giác ABC.
a) Chứng minh rằng hai đường tròn (B; BA) và (C; CA) cắt nhau. Gọi A’ là giao điểm khác A của hai đường tròn đó.
b) Chứng minh rằng A và A’ đối xứng nhau qua BC.
c) Biết rằng AA′=24cm,AB=15cm và AC=13cm. Tính độ dài BC.
Bài 17 :
Cho hai đường tròn (O; 17cm) và (O'; 10cm) cắt nhau tại A và B. Biết OO' = 21cm. Tính độ dài đoạn thẳng AB.
Bài 18 :
Cho hai đường tròn (O) và (O') có bán kính bằng nhau, cắt nhau tại A và B. Chứng minh tứ giác OAO'B là hình thoi; từ đó, suy ra AB cắt OO' tại trung điểm của mỗi đường.
Bài 19 :
Cho hai đường tròn (O; R) và (O’; R) cắt nhau tại hai điểm M, N với OO' = 24cm và MN = 10 cm (Hình 52).
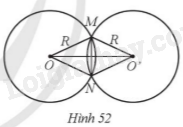
Khi đó, R bằng
A. 26 cm.
B. 13 cm.
C. 14 cm.
D. 34 cm.
Bài 20 :
Cho hai đường tròn (O) và (O’) cắt nhau tại A và B trong đó OA là tiếp tuyến của (O’). Biết rằng OA=20cm và O′A=15cm. Độ dài dây AB là:
A. 24cm.
B. 12cm.
C. 25cm.
D. 22cm.
Bài 21 :
Cho hai đường tròn (O; R) và (O’; r) với R=12cm,r=5cm,OO′=13cm.
a) Chứng minh hai đường tròn (O) và (O’) cắt nhau tại hai điểm A, B và OO’ là đường trung trực của AB.
b) Chứng minh AO là tiếp tuyến của (O’, r).
Bài 22 :
Cho hai đường tròn (A;R1),(B;R2), trong đó R2<R1. Biết rằng hai đường tròn (A) và (B) cắt nhau (H.5.43). Khi đó:
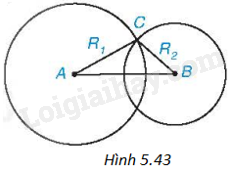
A. AB<R1−R2.
B. R1−R2<AB<R1+R2.
C. AB>R1+R2.
D. AB=R1+R2.
Bài 23 :
Cho hai đường tròn (O) và (O’) cắt nhau tại A và B. Một đường thẳng d đi qua A cắt (O) tại E và cắt (O’) tại F (E và F khác A). Biết điểm A nằm trong đoạn EF. Gọi I và K lần lượt là trung điểm của AE và AF (H.5.49).
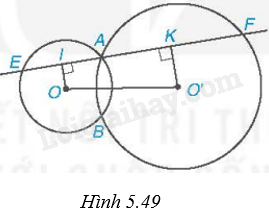
a) Chứng minh rằng tứ giác OO’KI là một hình thang vuông.
b) Chứng minh rằng IK=12EF.
c) Khi d ở vị trí nào (d vẫn qua A) thì OO’KI là một hình chữ nhật?
Bài 24 :
Cho hình vẽ. Chọn khẳng định đúng.
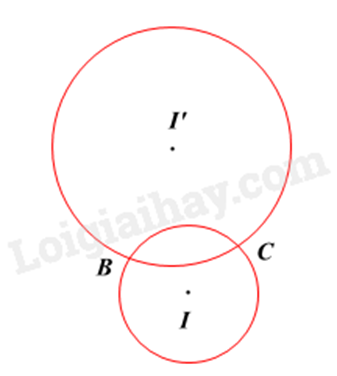
-
A.
Hai đường tròn (I) và (I′) tiếp xúc trong.
-
B.
Hai đường tròn (I) và (I′) tiếp xúc ngoài.
-
C.
Hai đường tròn (I) và (I′) cắt nhau.
-
D.
Hai đường tròn (I) và (I′) không giao nhau.
Bài 25 :
Cho hai đường tròn (O;20cm) và (O′;15cm) cắt nhau. Khi đó
-
A.
OO′<5cm.
-
B.
5cm<OO′<35cm.
-
C.
OO′>35cm.
-
D.
OO′=35cm.












