Nội dung từ Loigiaihay.Com
Cho tam giác ABC có AB = 9cm, AC = 12cm, BC = 15cm. Độ dài đường cao AH (H \( \in \) BC) của tam giác ABC là
-
A.
8,4cm.
-
B.
7,2cm.
-
C.
6,8cm.
-
D.
4,2cm.
Chứng minh tam giác ABC vuông. Sử dụng tính chất của tỉ số lượng giác để tính AH.
Vì \(A{B^2} + A{C^2} = {9^2} + {12^2} = 225 = {15^2} = B{C^2}\) nên tam giác ABC vuông tại A.
Khi đó \(\sin B = \frac{{AC}}{{BC}} = \frac{{12}}{{15}} = \frac{4}{5}\).
Mà tam giác ABH vuông tại H nên \(\sin B = \frac{{AH}}{{AB}} = \frac{{AH}}{9}\).
Suy ra \(\frac{{AH}}{9} = \frac{4}{5}\).
Do đó \(AH = 9.\frac{4}{5} = \frac{{36}}{5} = 7,2\left( {cm} \right)\).
Đáp án B
Đáp án : B

Các bài tập cùng chuyên đề
Cho tam giác $MNP$ vuông tại $M$. Khi đó $\cos \widehat {MNP}$ bằng
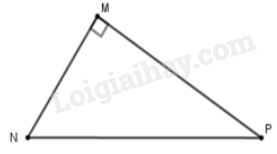
Cho $\alpha $ là góc nhọn bất kỳ. Chọn khẳng định đúng.
Cho $\alpha $ là góc nhọn bất kỳ. Chọn khẳng định sai.
Cho tam giác $ABC$ vuông tại $C$ có \(BC = 1,2\,cm,\,\,AC = 0,9\,cm.\) Tính các tỉ số lượng giác $\sin B;\cos B$ .
Cho tam giác $ABC$ vuông tại $A$ có \(BC = 8\,cm,\,\,AC = 6cm.\) Tính tỉ số lượng giác $\tan C$ (làm tròn đến chữ số thập phân thứ $2$ ).
Cho tam giác $ABC$ vuông tại $A$, đường cao $AH$ có \(CH = 4\,cm,\,BH = 3\,cm.\) Tính tỉ số lượng giác $\cos C$ (làm tròn đến chữ số thập phân thứ $2$ )
Cho $\alpha$ là góc nhọn. Tính \(\sin \alpha,\,\cot \alpha \) biết \(\cos \alpha = \dfrac{2}{5}\).
Cho $\alpha $ là góc nhọn bất kỳ. Khi đó $C = {\sin ^4}\alpha + {\cos ^4}\alpha $ bằng
Cho $\alpha $ là góc nhọn bất kỳ. Rút gọn $P = \left( {1 - {{\sin }^2}\alpha } \right).{\cot ^2}\alpha + 1 - {\cot ^2}\alpha $ ta được
Cho $\alpha $ là góc nhọn bất kỳ. Biểu thức $Q = \dfrac{{1 + {{\sin }^2}\alpha }}{{1 - {{\sin }^2}\alpha }}$ bằng
Cho $\tan \alpha = 2$. Tính giá trị của biểu thức $G = \dfrac{{2\sin \alpha + \cos \alpha }}{{\cos \alpha - 3\sin \alpha }}$
Cho tam giác nhọn \(ABC\) hai đường cao \(AD\) và \(BE\) cắt nhau tại \(H\). Biết \(HD:HA = 1:2\). Khi đó \(\tan \widehat {ABC}.\tan \widehat {ACB}\) bằng
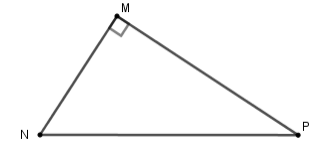 Bài 13 :
Bài 13 : Cho tam giác \(MNP\) vuông tại \(M\). Khi đó \(\tan \widehat {MNP}\) bằng
Cho tam giác \(ABC\) vuông tại \(C\) có \(AC = 1\,cm,\,\,BC = 2\,cm.\) Tính các tỉ số lượng giác \(\sin B;\cos B\)
Cho tam giác \(ABC\) vuông tại \(A\) có \(BC = 9\,cm,\,\,AC = 5cm.\) Tính tỉ số lượng giác \(\tan C\) (làm tròn đến chữ số thập phân thứ \(1\) )
Cho tam giác \(ABC\) vuông tại \(A\), đường cao \(AH\) có \(CH = 11\,cm,\,BH = 12\,cm.\) Tính tỉ số lượng giác \(\cos C\) (làm tròn đến chữ số thập phân thứ \(2\) )
Tính \(\sin \alpha ,\,\,\tan \alpha \) biết \(\cos \alpha = \dfrac{3}{4}\).
Cho \(\alpha \) là góc nhọn bất kỳ. Khi đó \(C={\sin ^6}\alpha + {\cos ^6}\alpha + 3{\sin ^2}\alpha {\cos ^2}\alpha \) bằng
Cho \(\alpha \) là góc nhọn bất kỳ. Cho \(P = \left( {1 - {{\sin }^2}\alpha } \right).{\tan ^2}\alpha + \left( {1 - {{\cos }^2}\alpha } \right){\cot ^2}\alpha \), chọn kết luận đúng.
Cho \(\alpha \) là góc nhọn bất kỳ. Biểu thức \(Q = \dfrac{{{{\cos }^2}\alpha - {{\sin }^2}\alpha }}{{\cos \alpha .\sin \alpha }}\) bằng
Cho \(\tan \alpha = 4\). Tính giá trị của biểu thức \(P = \dfrac{{3\sin \alpha - 5\cos \alpha }}{{4\cos \alpha + \sin \alpha }}\)
Cho tam giác nhọn \(ABC\) hai đường cao \(AD\) và \(BE\) cắt nhau tại \(H\). Biết \(HD:HA = 3:2\). Khi đó \(\tan \widehat {ABC}.\tan \widehat {ACB}\) bằng
Chọn kết luận đúng về giá trị biểu thức \(B = \dfrac{{{{\cos }^2}\alpha - 3{{\sin }^2}\alpha }}{{3 - {{\sin }^2}\alpha }}\) biết \(\tan \alpha = 3.\)
Cho tam giác \(ABC\) cân tại \(A\) có \(AB = AC = 13cm\); \(BC = 10cm\). Tính \(sinA\).
Cho tam giác \(ABC\) vuông tại \(A\) có \(AC = 3,AB = 4\). Khi đó \(\cos B\) bằng
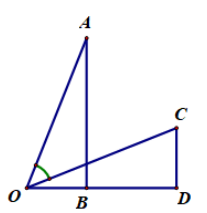
Cho hai tam giác vuông \(OAB\) và \(OCD\) như hình vẽ. Biết \(OB = CD = a\), \(AB = OD = b.\) Tính \(\cos \angle AOC\) theo \(a\) và \(b\).
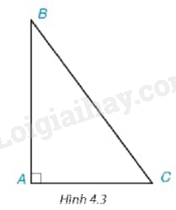
Xét góc C của tam giác ABC vuông tại A (H.4.3) . Hãy chỉ ra cạnh đối và cạnh kề của góc C.
Cho tam giác ABC vuông tại A và tam giác A’B’C’ vuông tại A’ có \(\widehat B = \widehat {B'} = \alpha .\) Chứng minh rằng:
a) \(\Delta ABC\backsim \Delta A'B'C';\)
b) \(\frac{{AC}}{{BC}} = \frac{{A'C'}}{{B'C'}};\frac{{AB}}{{BC}} = \frac{{A'B'}}{{B'C'}};\frac{{AC}}{{AB}} = \frac{{A'C'}}{{A'B'}};\frac{{AB}}{{AC}} = \frac{{A'B'}}{{A'C'}}\)
Cho tam giác ABC vuông tại A có AB = 5 cm, AC = 12 cm. Hãy tính các tỉ số lượng giác của góc B.
Cho tam giác ABC vuông tại A. Tính các tỉ số lượng giác sin, cosin, tang, cotang của các góc nhọn B và C khi biết:
a) AB = 8 cm, BC = 17 cm;
b) AC = 0,9 cm, AB = 1,2 cm.












