Đồ thị của hàm số $y = 2x + 1 + \frac{2}{{3x - 1}}$ có đường tiệm cận xiên là

Cho hàm số $y = f\left( x \right) = x - 1 + \frac{2}{{x + 1}}$ có đồ thị (C) và đường thẳng $y = x - 1$ như Hình 1.24.

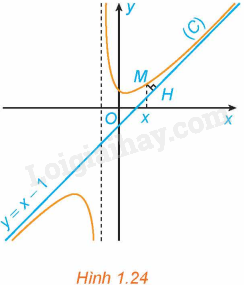
a) Với $x >  - 1$, xét điểm M (x; f(x)) thuộc (C). Gọi H là hình chiếu vuông góc của M trên đường thẳng $y = x - 1$. Có nhận xét gì về khoảng cách MH khi $x \to  + \infty$?

b) Chứng tỏ rằng $\mathop {\lim }\limits_{x \to  + \infty } \left[ {f\left( x \right) - \left( {x - 1} \right)} \right] = 0$. Tính chất này thể hiện trên Hình 1.24 như thế nào?

Tiệm cận xiên của đồ thị hàm số $y = \frac{{{x^2} + 2x - 2}}{{x + 2}}$ là

A. $y =  - 2$.

B. $y = 1$.

C. $y = x + 2$.

D. $y = x$.

Tìm tiệm cận xiên của đồ thị hàm số $y = f\left( x \right) = \frac{{{x^2} - 3x + 2}}{{x + 3}}$.

Chứng minh rằng đường thẳng $y =  - x$ là tiệm cận xiên của đồ thị hàm số $y = f\left( x \right) = \frac{{ - {x^2} - 2x + 3}}{{x + 2}}$.

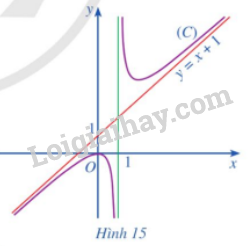
Cho hàm số $y = f\left( x \right) = x + 1 + \frac{1}{{x - 1}}$ có đồ thị $\left( C \right)$ và đường thẳng $y = x + 1$ (Hình 15). Tìm $\mathop {\lim }\limits_{x \to  + \infty } \left[ {f\left( x \right) - \left( {x + 1} \right)} \right];\mathop {\lim }\limits_{x \to  - \infty } \left[ {f\left( x \right) - \left( {x + 1} \right)} \right]$

Tiệm cận xiên của đồ thị hàm số $y = \frac{{{x^2} + 3x + 5}}{{x + 2}}$ là:
A. $y = x$.
B. $y = x + 1$.
C. $y = x + 2$.
D. $y = x + 3$.

Tìm tiệm cận xiên của đồ thị hàm số $y = \frac{{2{x^2} - 3x}}{{x + 5}}$

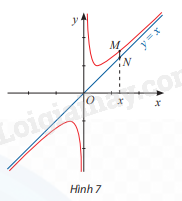
Cho đồ thị của hàm số $y = \frac{{{x^2} + 1}}{x}$ và đường thẳng y = x. Đường thẳng vuông góc với trục Ox tại điểm x cắt đồ thị hàm số tại điểm M và cắt đường thẳng y = x tại điểm N (Hình 7).

a) Tính $\mathop {\lim }\limits_{x \to  - \infty } (\frac{{{x^2} + 1}}{x} - x)$ và $\mathop {\lim }\limits_{x \to  + \infty } (\frac{{{x^2} + 1}}{x} - x)$

b) Tính MN theo x và nhận xét về MN khi $x \to  + \infty$ hoặc $x \to  - \infty$

Tiệm cận xiên của đồ thị hàm số $y = \frac{{2{x^3} + 3{x^2} - 3}}{{{x^2} - 1}}$ là đường thẳng có phương trình

A. $y = 2x + 3$              B. $y = x + 3$                C. $y = 2x + 1$              D. $y = x + 1$

Cho hàm số f(x) có đồ thị như hình dưới đây:

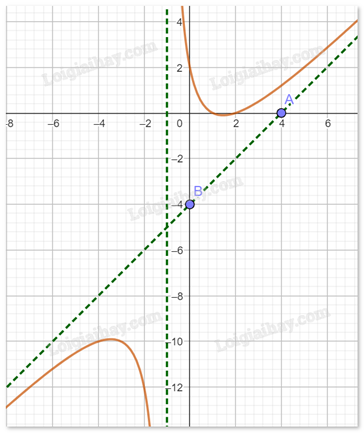
Đường tiệm cận xiên của đồ thị đã cho là đường thẳng:

Đường tiệm cận xiên của đồ thị hàm số $y = \frac{{{x^2} + 4x - 7}}{{x - 2}}$ là:

Đường tiệm cận xiên của đồ thị hàm số $y = \frac{{ - {x^2} + 4x - 1}}{{x + 3}}$ là:

Đường tiệm cận xiên của đồ thị hàm số $y = \frac{{2{x^2} - 9x + 3}}{{x + 2}}$ là:

Đường tiệm cận xiên của đồ thị hàm số $y = \frac{{{x^2} - 4x + 2}}{{ - 2x + 3}}$ là:

Đường tiệm cận xiên của đồ thị hàm số $y = \frac{{{x^2} + 3x}}{{x - 2}}$ là:

Đường tiệm cận xiên của đồ thị hàm số $y = \frac{{{x^2} + 2x - 1}}{x}$ là:

Tiệm cận xiên của đồ thị hàm số $y = 2x - 1 - \frac{2}{{x + 1}}$ là đường thẳng:

A. $y = 2x$.                     

B. $y = x + 1$.                

C. $y = 2x - 1$.               

D. $y =  - 2x + 1$.

Tiệm cận xiên của đồ thị hàm số $y = \frac{{3{{\rm{x}}^2} + x - 2}}{{x - 2}}$ là đường thẳng:

A. $y =  - 3{\rm{x}} + 7$  

B. $y = 3{\rm{x}} + 7$

C. $y = 3{\rm{x}} - 7$

D. $y =  - 3{\rm{x}} - 7$

Cho hàm số $y = \frac{{{x^2} - 2{\rm{x}} + 6}}{{x + 1}}$.

A. Đồ thị hàm số có một tiệm cận xiên là $y = x - 3$.

B. Đồ thị hàm số có một tiệm cận xiên là $y = x + 3$.

C. Đồ thị hàm số có một tiệm cận xiên là $y = x + 1$.

D. Đồ thị hàm số không có tiệm cận xiên.

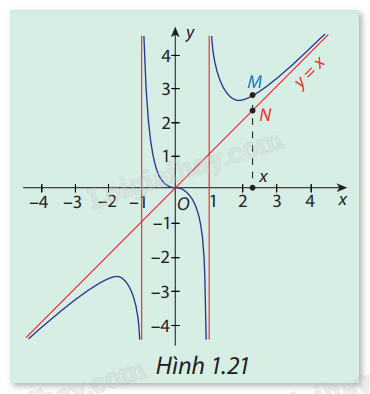
Trong Hình 1.21, đường cong là đồ thị ( C ) của hàm số $y = f(x) = x + \frac{x}{{{x^2} - 1}}$ và đường thẳng $\Delta :y = x$ . Gọi M, N lần lượt là hai điểm thuộc ( C ) và$\Delta$ có cùng hoành độ x, với x > 1 hoặc x < -1. Nhận xét về độ dài của đoạn MN khi$x \to  - \infty$ và $x \to  + \infty .$

Sử dụng ghi chú ở trên, tìm tiệm cận xiên của đồ thị hàm số $y = f(x) = \frac{{ - {x^2} - 3x - 3}}{{x + 1}}$.

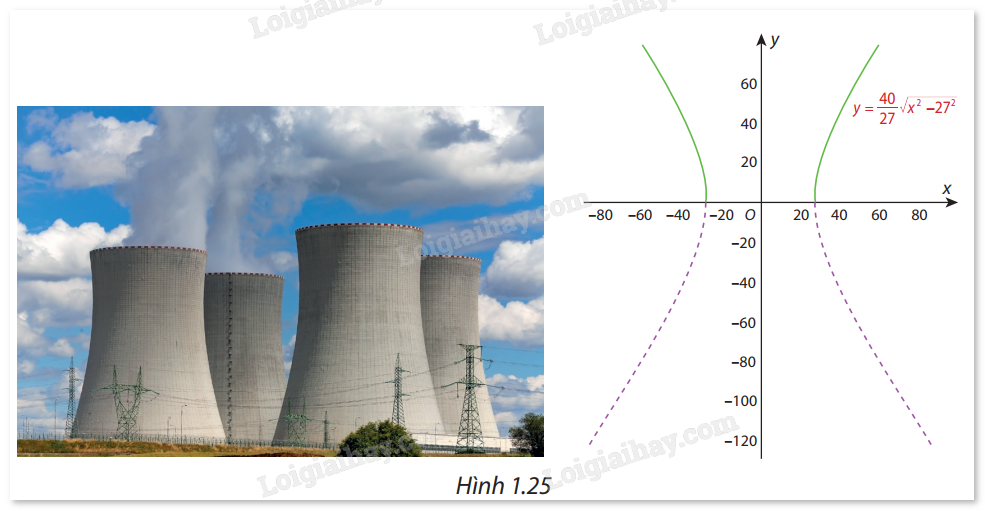
Một ống khói của nhà máy điện hạt nhân có mặt cắt là một hypebol (H) có phương trình chính tắc là $\frac{{{x^2}}}{{{{27}^2}}} - \frac{{{y^2}}}{{{{40}^2}}} = 1$ (Hình 1.25). Hét hai nhánh bên trên Ox của (H) là đồ thị (C) của hàm số $y = \frac{{40}}{{27}}\sqrt {{x^2} - {{27}^2}}$ (phần nét liền đậm). Chứng minh rằng đường thẳng $y = \frac{{40}}{{27}}x$ là một đường tiệm cận của (C). Hãy chỉ ra them một đường tiệm cận xiên khác của (C).

Cho hàm số $f(x) = x + 2 - \frac{1}{{x - 1}}$. Tiệm cận xiên của đồ thị đã cho là đường thẳng

Cho hàm số $f(x) = x - 3 + \frac{5}{{x - 2}}$. Tiệm cận xiên của đồ thị đã cho là đường thẳng

Cho hàm số $f(x) = x + 1 + \frac{3}{{x - 6}}$. Tiệm cận xiên của đồ thị đã cho là đường thẳng

Cho hàm số $f(x) = x - 3 + \frac{1}{{2 - x}}$. Tiệm cận xiên của đồ thị đã cho là đường thẳng

Tiệm cận xiên của đồ thị hàm số $y = \frac{{{x^2} - 2x + 3}}{{x + 1}}$ là:

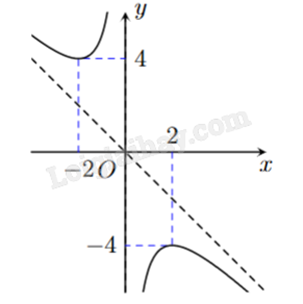
Cho hàm số $y = \frac{{a{x^2} + bx + c}}{x}$ $(ac \ne 0)$ có đồ thị như hình vẽ. Đường tiệm cận xiên của đồ thị hàm số đã cho là đường thẳng

Cho hàm số $y = \frac{{a{x^2} + bx + c}}{{mx + n}}$ (với $a \ne 0$, $m \ne 0$) có đồ thị như hình vẽ dưới đây.

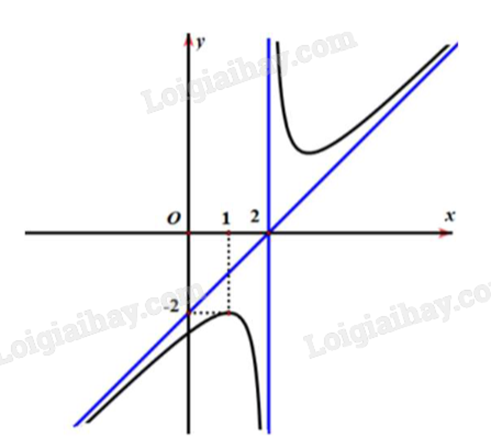
Phương trình đường tiệm cận xiên của đồ thị hàm số đã cho là

Cho hàm số $y = \frac{{a{x^2} + bx + c}}{{dx + e}}$ (với $a,b,c,d,e \in \mathbb{R}$, $ad \ne 0$) có đồ thị như hình vẽ.

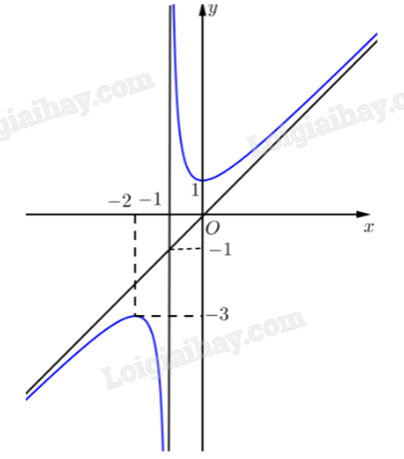
Tiệm cận xiên của đồ thị hàm số đã cho là