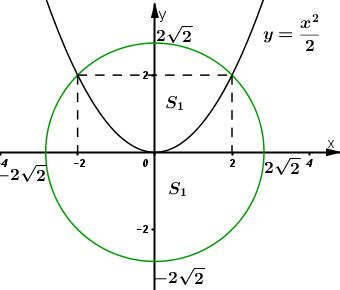
Giải bài 3 trang 121 SGK Giải tích 12

Đề bài

Parabol $y = {{{x^2}} \over 2}$ chia hình tròn có tâm tại gốc tọa độ, bán kính $2\sqrt2$ thành hai phần. Tìm tỉ số diện tích của chúng.

Lời giải chi tiết

Đường tròn đã cho có phương trình: ${x^{2}} + {\rm{ }}{y^2} = {\rm{ }}8.$

Từ đó ta có: $y =  \pm \sqrt {8 - {x^2}}$

Tọa độ giao điểm của $(C)$ và $(P)$ là nghiệm của hệ phương trình: 

$\left\{ \matrix{ {x^2} = 2y \hfill \cr {x^2} + {y^2} = 8 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{ {y^2} + 2y - 8 = 0 \hfill \cr {x^2} = 2y \hfill \cr} \right.$

$\Leftrightarrow \left\{ \matrix{ \left[ \begin{array}{l} y = 2\;\;\left( {tm} \right)\\y = - 4\;\;\left( {ktm} \right)\end{array} \right. \hfill \cr x^2=2y \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{y = 2 \hfill \cr x = \pm 2 \hfill \cr} \right.$

Gọi $S_1$ và $S_2$ là diện tích hai phần của đường tròn được chia bởi parabol $(P)$ như hình vẽ.

Khi đó ta có:

$\begin{array}{l}{S_1} = \int\limits_{ - 2}^2 {\left( {\sqrt {8 - {x^2}}  - \frac{{{x^2}}}{2}} \right)dx} \\ = \int\limits_{ - 2}^2 {\sqrt {8 - {x^2}} dx}  - \int\limits_{ - 2}^2 {\frac{{{x^2}}}{2}dx} \\ = {I_1} - {I_2}\end{array}$

Tính ${I_1} = \int\limits_{ - 2}^2 {\sqrt {8 - {x^2}} dx}$

Đặt $x = 2\sqrt 2 \sin t \Rightarrow dx = 2\sqrt 2 {\mathop{\rm costdt}\nolimits}$

Đổi cận:

$\eqalign{ & x = -2 \Rightarrow t = -{\pi \over 4} \cr & x = 2 \Rightarrow t = {\pi \over 4} \cr}$

$\begin{array}{l}{I_1} = \int\limits_{ - \frac{\pi }{4}}^{\frac{\pi }{4}} {\sqrt {8 - 8{{\sin }^2}t} .2\sqrt 2 \cos tdt} \\ = \int\limits_{ - \frac{\pi }{4}}^{\frac{\pi }{4}} {\sqrt {8\left( {1 - {{\sin }^2}t} \right)} .2\sqrt 2 \cos tdt} \\ = \int\limits_{ - \frac{\pi }{4}}^{\frac{\pi }{4}} {\sqrt {8{{\cos }^2}t} .2\sqrt 2 \cos tdt} \\ = \int\limits_{ - \frac{\pi }{4}}^{\frac{\pi }{4}} {2\sqrt 2 \cos t.2\sqrt 2 \cos tdt} \\ = \int\limits_{ - \frac{\pi }{4}}^{\frac{\pi }{4}} {8{{\cos }^2}tdt} \\ = \int\limits_{ - \frac{\pi }{4}}^{\frac{\pi }{4}} {8.\frac{{1 + \cos 2t}}{2}dt} \\ = 4\int\limits_{ - \frac{\pi }{4}}^{\frac{\pi }{4}} {\left( {1 + \cos 2t} \right)dt} \\ = 4\left. {\left( {t + \frac{{\sin 2t}}{2}} \right)} \right|_{ - \frac{\pi }{4}}^{\frac{\pi }{4}}\\ = 4\left( {\frac{\pi }{4} + \frac{{\sin \frac{\pi }{2}}}{2} + \frac{\pi }{4} - \frac{{\sin \left( { - \frac{\pi }{2}} \right)}}{2}} \right)\\ = 2\pi  + 4\end{array}$

Tính ${I_2} = \int\limits_{ - 2}^2 {\frac{{{x^2}}}{2}dx}$

$\begin{array}{l}{I_2} = \int\limits_{ - 2}^2 {\frac{{{x^2}}}{2}dx}  = \frac{1}{2}.\left. {\frac{{{x^3}}}{3}} \right|_{ - 2}^2\\ = \frac{1}{2}\left( {\frac{8}{3} - \frac{{ - 8}}{3}} \right) = \frac{8}{3}\end{array}$

Do đó ${S_1} = {I_1} - {I_2} = 2\pi  + 4 - \frac{8}{3} = 2\pi  + \frac{4}{3}$

Diện tích hình tròn là: $\pi R^2=8\pi$

${S_2} = 8\pi  - {S_1}$$= 8\pi-2\pi  - {4 \over 3}=6\pi-{4\over 3}.$

Vậy ${{{S_2}} \over {{S_1}}} = \frac{{6\pi  - \frac{4}{3}}}{{2\pi  + \frac{4}{3}}} = \frac{{18\pi  - 4}}{{6\pi  + 4}} = {{9\pi  - 2} \over {3\pi  + 2}}$ hay $\dfrac{{{S_1}}}{{{S_2}}} = \dfrac{{3\pi  + 2}}{{9\pi  - 2}}$

HocTot.Nam.Name.Vn