Nội dung từ Loigiaihay.Com
Thực hiện phép tính nhân \(\left( {2x - y} \right)\left( {x - y} \right)\) ta được
-
A.
\(2{x^2} + 3xy - {y^2}\).
-
B.
\(2{x^2} - 3xy + {y^2}\).
-
C.
\(2{x^2} - xy + {y^2}\).
-
D.
\(2{x^2} + xy - {y^2}\).
Muốn nhân một đa thức với một đa thức, ta nhân mỗi hạng tử của đa thức này với từng hạng tử của đa thức kia rồi cộng các tích với nhau.
Ta có:
\(\left( {2x - y} \right)\left( {x - y} \right) = 2{x^2} - xy - 2xy + {y^2} = 2{x^2} - 3xy + {y^2}\).
Đáp án B.
Đáp án : B

Các bài tập cùng chuyên đề
Chọn câu đúng.
Hãy nhớ lại quy tắc nhân hai đa thức một biến bằng cách thực hiện phép nhân:
\(\left( {2x + 3} \right).\left( {{x^2} - 5x + 4} \right)\)
Bằng cách tương tự, hãy làm phép nhân \(\left( {2x + 3y} \right).\left( {{x^2} - 5xy + 4{y^2}} \right)\).
Thực hiện phép nhân:
a) \(\left( {2x + y} \right)\left( {4{x^2} - 2xy + {y^2}} \right)\);
b) \(\left( {{x^2}{y^2} - 3} \right)\left( {3 + {x^2}{y^2}} \right)\).
Xét biểu thức đại số với hai biến k và m sau:
\(P = \left( {2k - 3} \right)\left( {3m - 2} \right) - \left( {3k - 2} \right)\left( {2m - 3} \right)\)
a) Rút gọn biểu thức P.
b) Chứng minh rằng tại mọi giá trị nguyên của k và m, giá trị của biểu thức P luôn là một số nguyên chia hết cho 5.
Làm tính nhân:
a) \(\left( {{x^2} - xy + 1} \right)\left( {xy + 3} \right)\)
b) \(\left( {{x^2}{y^2} - \dfrac{1}{2}xy + 2} \right)\left( {x - 2y} \right)\)
Chứng minh đẳng thức sau: \(\left( {2x + y} \right)\left( {2{x^2} + xy - {y^2}} \right) = \left( {2x - y} \right)\left( {2{x^2} + 3xy + {y^2}} \right)\).
Bà Khanh dự định mua x hộp sữa, mỗi hộp giá y đồng. Nhưng khi đến cửa hàng, bà Khanh thấy giá sữa giảm 1 500 đồng mỗi hộp nên quyết định mua thêm 3 hộp nữa.
Tìm đa thức biểu thị số tiền bà Khanh phải trả cho tổng số hộp sữa đã mua.
Bà Khanh dự định mua x hộp sữa, mỗi hộp giá y đồng. Nhưng khi đến cửa hàng, bà Khanh thấy giá sữa giảm 1 500 đồng mỗi hộp nên quyết định mua thêm 3 hộp nữa.
Tìm đa thức biểu thị số tiền bà Khanh phải trả cho tổng số hộp sữa đã mua.
Thực hiện các phép nhân:
a) \(\left( { - 5{a^4}} \right)\left( {{a^2}b - a{b^2}} \right)\)
b) \(\left( {x + 2y} \right)\left( {x{y^2} - 2{y^3}} \right)\)
Thực hiện các phép nhân:
a) \(\left( {x - y} \right)\left( {x - 5y} \right)\)
b) \(\left( {2x + y} \right)\left( {4{x^2} - 2xy + {y^2}} \right)\)
Kết quả của phép nhân \((x + y - 1)(x + y + 1)\) là:
A. \({x^2} - 2xy + {y^2} + 1\)
B. \({x^2} + 2xy + {y^2} - 1\)
C. \({x^2} - 2xy + {y^2} - 1\)
D. \({x^2} + 2xy + {y^2} + 1\)
Kết quả của phép nhân \((2x + 1)(4{x^2} - 2x + 1)\) là:
A. \(8{x^3} - 1\)
B. \(4{x^3} + 1\)
C. \(8{x^3} + 1\)
D. \(2{x^2} + 1\)
Thực hiện các phép tính sau:
a) \({x^2}y\left( {5xy - 2{x^2}y - {y^2}} \right)\)
b) \(\left( {x - 2y} \right)\left( {2{x^2} + 4xy} \right)\)
a) Tính tích: \(\left( {x + 1} \right).\left( {{x^2} - x + 1} \right)\)
b) Nêu quy tắc nhân hai đa thức trong trường hợp một biến.
Tính: \({\left( {x - y} \right)}{\left( {x - y} \right)}\)
Giải thích vì sao ta có thể viết:
\(\left( {x + 2y} \right).\left( {2x - y} \right) = x.2x + y.\left( { - y} \right) + 2y.2x + 2y.\left( { - y} \right) = 2{x^2} - xy + 4xy - 2{y^2} = 2{x^2} + 3xy - 2{y^2}\)
Tính tích của hai đa thức \(G = {x^2} - 3y + 8\) và \(H = {y^2} - 2x\)
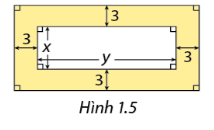
Trong phần Khởi động, hãy tính diện tích của phần được tô màu trong Hình 1.5 theo \(x\) và \(y\).
Thực hiện các phép tính sau:
a) \(\left( {x - 4} \right)\left( {{y^3} + 2y - 3} \right)\);
b) \(\left( {{x^2} - xy + {y^2}} \right)\left( {x + y} \right)\)
Thực hiện các phép nhân:
a) \(\left( {x + 3y} \right)\left( {x - 2y} \right)\);
b) \(\left( {2x - y} \right)\left( {y - 5x} \right)\);
c) \(\left( {2x - 5y} \right)\left( {{y^2} - 2xy} \right)\);
d) \(\left( {x - y} \right)\left( {{x^2} - xy - {y^2}} \right)\).
Thực hiện phép tính:
a) \(\left( {x - 2y} \right)\left( {{x^2}z + 2xyz + 4{y^2}z} \right)\)
b) \(\left( {{x^2} - \frac{1}{3}xy + \frac{1}{9}{y^2}} \right)\left( {x + \frac{1}{3}y} \right)\).
Tìm tích của hai đa thức:
a) \(2{x^4} - {x^3}y + 6x{y^3} + 2{y^4}\) và \({x^4} + 3{x^3}y - {y^4}\);
b) \({x^3}y + 0,4{x^2}{y^2} - x{y^3}\) và \(5{x^2} - 2,5xy + 5{y^2}\).
Chứng minh rằng giá trị của biểu thức sau không phụ thuộc vào giá trị của biến:
\(P = {x^4} - \left( {x - y} \right)\left( {x + y} \right)\left( {{x^2} + {y^2}} \right) - {y^4}\).
Rút gọn biểu thức:
a) \(\left( {x - y} \right)\left( {y + z} \right)\left( {z + x} \right) + \left( {x + y} \right)\left( {y - z} \right)\left( {z + x} \right) + \left( {x + y} \right)\left( {y + z} \right)\left( {z - x} \right)\);
b) \(\left( {2x + y} \right)\left( {2y + z} \right)\left( {2z + x} \right) - \left( {2x - y} \right)\left( {2y - z} \right)\left( {2z - x} \right)\).
Tích của một đa thức bậc 3 và một đa thức bậc 2 là một đa thức
A. bậc 5.
B. bậc 6.
C. bậc nhỏ hơn 5.
D. bậc lớn hơn 6.
Thu gọn các tích \(A = \left( {{x^2}y + x{y^2}} \right)\left( {{x^2} - xy + {y^2}} \right)\) và \(B = \left( {x - y} \right)\left( {{x^3}y + {x^2}{y^2} + x{y^3}} \right)\), ta được:
A. \(A = {x^4}y - x{y^4}\) và \(B = {x^4}y + x{y^4}\).
B. \(A = {x^4}y + x{y^4}\) và \(B = {x^4}y - x{y^4}\).
C. \(A = x{y^4} - {x^4}y\) và \(B = {x^4}y + x{y^4}\).
D. \(A = {x^4}y + x{y^4}\) và \(B = x{y^4} - {x^4}y\).
Thực hiện phép nhân
a) \(\frac{2}{5}{x^2}y\left( {5{x^2}y - 10x{y^2} + 2{y^3}} \right)\);
b) \(\left( {{x^2} - 2xy} \right)\left( {{x^3} + 3{x^2}y - 5x{y^2} - {y^3}} \right)\).
Một chiếc khăn trải bàn có dạng hình chữ nhật \(ABCD\) được thêu một họa tiết có dạng hình thoi \(MNPQ\) ở giữa với \(MP = x\left( {cm} \right);NQ = y\left( {cm} \right)\left( {x > y > 0} \right)\) như Hình 5. Viết đa thức biểu thị diện tích phần còn lại của chiếc khan trải bàn đó.

Làm tính nhân:
a) \(\left( {{x^2}\;-xy + 1} \right)\left( {xy + 3} \right)\).
b) \(\left( {{x^2}{y^2} - \frac{1}{2}xy + 2} \right)\left( {x - 2y} \right)\).












