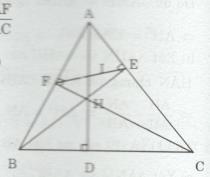
Bài tập 25 trang 92 Tài liệu dạy – học Toán 8 tập 2Giải bài tập Cho tam giác ABC có ba góc nhọn, các đường cao AD, BE, CF cắt nhai tại H. GÓP Ý HAY - NHẬN NGAY QUÀ CHẤT Gửi góp ý cho HocTot.Nam.Name.Vn và nhận về những phần quà hấp dẫn Đề bài Cho tam giác ABC có ba góc nhọn, các đường cao AD, BE, CF cắt nhai tại H. a) Chứng minh rằng tam giác AEF đồng dạng với tam giác ABC. b) Chứng minh rằng AD.HD = DB.DC. c) Gọi I là giao điểm của AH với EF. Chứng minh rằng tam giác IAF đồng dạng với tam giác IEH. Lời giải chi tiết a) Xét ∆AEB và ∆AFC có: ^EAF (chung) và ^AEB=^AFC(=90∘) Do đó ΔAEB∼ΔAFC(g.g) ⇒AEAF=ABAC ⇒AEAB=AFAC Xét ∆AEF và ∆ABC có: AEAB=AFAC và góc EAF (chung) Do đó ΔAEF∼ΔABC(c.g.c) b) Xét ∆ACD và ∆BHD có: ^ADC=^HDB(=90∘) Và ^CAD=^HBD (cùng phụ với góc ACB) Do đó ΔACD∼ΔBHD(g.g) ⇒ADDB=DCHD ⇒AD.HD=DB.DC c) Ta có ^AFI=^ACB(ΔAEF∼ΔABC) Mà ^IHE=^ACB (cùng phụ với góc HAE) nên ^AFI=^IHE Xét ∆IAF và ∆IEH có: ^AFI=^IHE và ^AIF=^HIE (đối đỉnh) Do đó ΔIAF∼ΔIEH(g.g) HocTot.Nam.Name.Vn
>> Học trực tuyến lớp 8 trên Tuyensinh247.com. Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Cam kết giúp học sinh lớp 8 học tốt, hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link
|