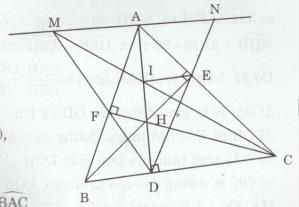
Bài tập 29 trang 92 Tài liệu dạy – học Toán 8 tập 2

Đề bài

Cho tam giác nhọn ABC, các đường cao AD, BE, CF cắt nhau tại H.

a) Chứng minh rằng : $\Delta BDA \sim \Delta BFC$ và BD.BC = BF.BA

b) Chứng minh rằng $\widehat {BDF} = \widehat {BAC}$ .

c) CHứng minh rằng BH.BE = BD.BC và $BH.BE{\rm{ }} + {\rm{ }}CH.CF{\rm{ }} = B{C^2}$ .

d) Đường thẳng qua A song song với BC cắt tia DF tại M. Gọi I là giao điểm của CM và AD. Chứng minh rằng IE // BC.

Lời giải chi tiết

a) Xét ∆BDA và ∆BFC có:

$\widehat {DBA}$ (chung), $\widehat {BDA} = \widehat {BFC}( = 90^\circ )$

Do đó $\Delta BDA \sim \Delta BFC(g.g)$

$\Rightarrow {{BD} \over {BF}} = {{BA} \over {BC}}$

$\Rightarrow BD.BC = BF.BA$

b) Xét ∆BDF và ∆BAC có: $\widehat {DBF}(chung),$

${{BD} \over {BA}} = {{BF} \over {BC}}$ (vì BD.BC = BF.BA)

Do đó $\Delta BDF \sim \Delta BAC(c.g.c)$

$\Rightarrow \widehat {BDF} = \widehat {BAC}$

c) Xét ∆BDH và ∆BEC có: $\widehat {DBH}(chung),\widehat {BDH} = \widehat {BEC}( = 90^\circ )$

Do đó $\Delta BDH \sim \Delta BEC(g.g)$

$\Rightarrow {{BD} \over {BE}} = {{BH} \over {BC}}$

$\Rightarrow BH.BE = BD.BC$

Tương tự có $\Delta CDH \sim \Delta CFB$

$\Rightarrow {{CH} \over {BC}} = {{CD} \over {CF}}$

$\Rightarrow CH.CF = CD.BC$

Do đó $BH.BE + CH.CF$$\,= BD.BC + CD.BC$$\, = BC.(BD + CD) = BC.BC= {BC^2}$

d) Gọi N là giao điểm của DE và AM, ta có $\widehat {BDF} = \widehat {BAC}(\Delta BDF \sim \Delta BAC)$

Tương tự $\widehat {CDE} = \widehat {CAB}$

Do đó $\widehat {BDF} = \widehat {CDE}.$

Mà $\widehat {BDF} + \widehat {ADM} = \widehat {CDE} + \widehat {ADN}( = 90^\circ )$

$\Rightarrow \widehat {ADM} = \widehat {ADN}$

Mặt MN // BC, $AD \bot BC \Rightarrow MN \bot AD$

∆DMN có DA là đường cao, đường phân giác

$\Rightarrow \Delta DMN$ cân tại D => AM = AN

Xét ∆IDC có: AM // CD $\Rightarrow {{AM} \over {CD}} = {{AI} \over {DI}}$ (hệ quả của định lí Thales)

Xét ∆EDC có: CD // AN $\Rightarrow {{AN} \over {CD}} = {{AE} \over {CE}}$ (hệ quả của định lí Thales) $\Rightarrow {{AI} \over {DI}} = {{AE} \over {CE}}$

Xét ∆AND có: ${{AI} \over {DI}} = {{AE} \over {CE}} \Rightarrow IE//AN$ (định lí Thales đảo)

Ta có IE // AN và AN // BC => IE // BC

HocTot.Nam.Name.Vn