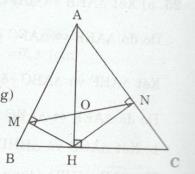
Bài tập 23 trang 92 Tài liệu dạy – học Toán 8 tập 2Giải bài tập Cho tam giác ABC có ba góc nhọn, đường cao AH Đề bài Cho tam giác ABC có ba góc nhọn, đường cao AH (H∈BC). Vẽ HM⊥AB,HN⊥AC(M∈AB,N∈AC) a) Chứng minh rằng ΔAMH∼ΔAHB. Suy ra AH2 = AM.AB. b) Chứng minh rằng AM.AB = AN.AC. c) Chứng minh ΔANM∼ΔABC. d) Gọi O là giao điểm của AH với MN. Chứng minh OA.OH = OM.ON. Lời giải chi tiết a) Xét ∆AMH và ∆AHB có: ^MAH chung và ^AMH=^AHB(=90∘) Do đó ΔAMH∼ΔAHB(g.g)⇒AHAB=AMAH ⇒AH2=AM.AB(1) b) Xét ∆AHN và ∆AHC có: ^HAN chung và ^ANH=^AHC(=90∘) ⇒ΔAHN∼ΔACH(g.g) ⇒AHAC=ANAH⇒AH2=AN.AC(2) Từ (1) và (2) suy ra AM.AB = AN.AC c) Xét ∆ANM và ∆ABC có: AMAC=ANAB (vì AM.AB = AN.AC) và góc MAN (chung) Do đó ΔANM∼ABC(c.g.c) d) Ta có ^AMN=^ACB(ΔANM∼ΔABC) và ^AHN=^ACB(ΔAHN∼ΔACH) ⇒^AMN=^AHNhay^AMO=^OHN Xét ∆AMO và ∆OHN có ^AOM=^NOH (đối đỉnh) và ^AMO=^OHN Do đó ΔAMO∼ΔNHO(g.g) ⇒OAON=OMOH ⇒OA.OH=OM.ON HocTot.Nam.Name.Vn
|