Đề bài

Năm nay tuổi cha 39 tuổi và gấp 3 lần tuổi con năm ngoái. Vậy năm nay tuổi con là

Phương pháp giải

Gọi tuổi con hiện tại là x.

Lập phương trình.

Giải phương trình để tìm tuổi con. Kiểm tra kết quả.

Lời giải của GV HocTot.Nam.Name.Vn

Gọi tuổi của con hiện tại là x $\left( {x > 1,x \in N*} \right)$

Vì năm nay cha 39 tuổi và gấp 3 lần tuổi con năm ngoái nên ta có phương trình:

$\begin{array}{l}3\left( {x - 1} \right) = 39\\x - 1 = 13\\x = 14(TM)\end{array}$

Vậy năm nay con 14 tuổi.

Đáp án C.

Đáp án : C

Báo lỗi - Góp ý

Các bài tập cùng chuyên đề

Phương trình $x + 5 = x + 5$ có

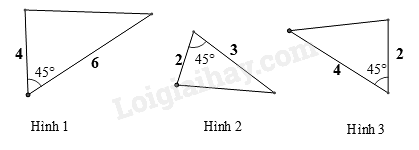
Hãy chỉ ra cặp tam giác đồng dạng trong các tam giác sau

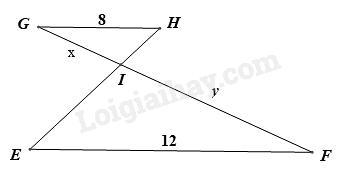
Cho $\Delta GHI\backsim \Delta FEI$ có các kính thước như hình vẽ, khi đó tỉ số độ dài của y và x bằng:

Giải các phương trình sau:

a) $2x - 4 = 3x + 1$

b) $7\left( {5 - x} \right) = 11 - 5x$

c) $\frac{5}{6} + \frac{x}{4} = 2 - \frac{x}{3}$

d) $\frac{{2\left( {x + 1} \right)}}{3} = \frac{{1 + 3x}}{4} + \frac{1}{2}$

Cho $\Delta ABC$ vuông tại A có $AB = 6cm$ và $AC = 8cm$. Đường phân giác của góc ABC cắt AC tại D. Từ C kẻ $CE \bot BD$ kẻ E.

a) Tính độ dài BC và tỉ số $\frac{{AD}}{{DC}}$.

b) Chứng minh $\Delta ABD\backsim \Delta EBC$. Từ đó suy ra $BD.EC = AD.BC$.

c) Chứng minh $\frac{{CD}}{{BC}} = \frac{{CE}}{{BE}}$.

d) Gọi EH là đường cao của $\Delta EBC$. Chứng minh $CH.HB = ED.EB$.