Nội dung từ Loigiaihay.Com
Cho \(\frac{a}{{b + c}} + \frac{b}{{c + a}} + \frac{c}{{a + b}} = 1\). Chứng minh \(\frac{{{a^2}}}{{b + c}} + \frac{{{b^2}}}{{c + a}} + \frac{{{c^2}}}{{a + b}} = 0\)
Nhân cả 2 vế của \(\frac{a}{{b + c}} + \frac{b}{{c + a}} + \frac{c}{{a + b}} = 1\) với \(a + b + c\) rồi thu gọn được điều phải chứng minh
Nhân cả 2 vế của \(\frac{a}{{b + c}} + \frac{b}{{c + a}} + \frac{a}{{a + b}} = 1\) với \(a + b + c\) ta được
\(\frac{{{\rm{a}}\left( {{\rm{a}} + {\rm{b}} + {\rm{c}}} \right)}}{{{\rm{b}} + {\rm{c}}}} + \frac{{{\rm{b}}\left( {{\rm{a}} + {\rm{b}} + {\rm{c}}} \right)}}{{{\rm{c}} + {\rm{a}}}} + \frac{{{\rm{c}}\left( {{\rm{a}} + {\rm{b}} + {\rm{c}}} \right)}}{{{\rm{a}} + {\rm{b}}}} = {\rm{a}} + {\rm{b}} + {\rm{c}}\)
\(\frac{{{a^2} + a\left( {b + c} \right)}}{{b + c}} + \frac{{{b^2} + b\left( {c + a} \right)}}{{c + a}} + \frac{{{c^2} + c\left( {a + b} \right)}}{{a + b}} = a + b + c\)
\(\frac{{{a^2}}}{{b + c}} + a + \frac{{{b^2}}}{{c + a}} + b + \frac{{{c^2}}}{{a + b}} + c = a + b + c\)
\(\frac{{{{\rm{a}}^2}}}{{{\rm{\;b}} + {\rm{c}}}} + \frac{{{{\rm{b}}^2}}}{{{\rm{c}} + {\rm{a}}}} + \frac{{{{\rm{c}}^2}}}{{{\rm{a}} + {\rm{b}}}} = 0\left( {{\rm{dpcm}}} \right)\)

Các bài tập cùng chuyên đề
Một tàu du lịch đi từ Hải Phòng đến Quảng Ninh với quang đường dài \(50{\rm{\;km}}/{\rm{h}}\). Vận tốc của dòng nước là \(3{\rm{\;km}}/{\rm{h}}\). Gọi vận tốc thực của tàu là \(x{\rm{\;km}}/{\rm{h}}\). Hãy biểu diễn thời gian tàu đi ngược dòng từ Quảng Ninh tới Hải Phòng.
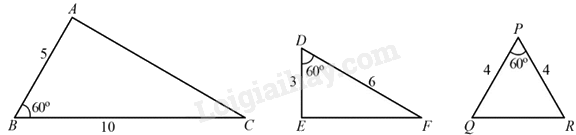
Quan sát hình sau và chỉ ra một cặp tam giác đồng dạng:
Đáp án nào dưới đây không là phương trình bậc nhất một ẩn?
Điều kiện xác định của phân thức \(\frac{{\left( {x - 1} \right)\left( {x + 3} \right)}}{{{x^2} - 1}}\) là:
Chọn khẳng định sai.
Hai tam giác nào không đồng dạng khi biết độ dài các cạnh của hai tam giác lần lượt là:
Kết quả của phép chia \(\frac{{a - 2b}}{{16}}:\frac{{2a - 4b}}{{12}}\) bằng:
Nếu 2 tam giác \({\rm{ABC}}\) và \({\rm{DEF}}\) có \(\widehat A = \widehat D,\widehat C = \widehat F\) thì:
Tổng các nghiệm của hai phương trình \( - 6\left( {1,5 - 2x} \right) = 3\left( { - 15 + 2x} \right);5x + 10 = 0\) bằng:
Cho biết một nửa đàn bò đang gặm cỏ trên cánh đồng, \(\frac{1}{3}\) đàn bò đang nằm nghỉ gần đó, còn lại 4 con đang uống nước ở ao. Tính số bò hiện có trong đàn.
Cho biểu thức: \(B = \frac{1}{{x + 1}} - \frac{{{x^3} - x}}{{{x^2} + 1}} \cdot \left( {\frac{1}{{{x^2} + 2x + 1}} - \frac{1}{{{x^2} - 1}}} \right)\) (ĐKXĐ: \(\left. {x \ne \pm 1} \right)\)
a) Rút gọn \(B\)
b) Tính giá trị của \(B\) tại \(x = - 2\)
c) Với giá trị nào của \(x\) thì \(B = 1\)
Giải các phương trình sau:
a) \(\frac{{9x + 5}}{6} = 1 - \frac{{6 + 3x}}{8}\);
b) \(\frac{{x + 1}}{4} = \frac{1}{2} + \frac{{2x + 1}}{5}\);
c) \(\frac{{2\left( {x + 1} \right)}}{3} = \frac{3}{2} - \frac{{1 - 2x}}{4}\).
Tổng số học sinh khối 8 và khối 9 của một trường là 580 em, trong đó có \(256\) em là học sinh giỏi. Tính số học sinh của mỗi khối, biết rằng số học sinh giỏi khối 8 chiếm tỉ lệ \(40{\rm{\% }}\) số học sinh khối 8, số học sinh giỏi khối 9 chiếm tỉ lệ 48% số học sinh khối 9.
Cho \(\Delta ABC\) có các đường cao \({\rm{BD}}\) và \({\rm{CE}}\) cắt nhau tại \({\rm{H}}\). Chứng minh:
a) \(\Delta HBE\) đồng dạng với \(\Delta HCD\).
b) \(\widehat {HDE} = \widehat {HAE}\).












