Nội dung từ Loigiaihay.Com
Cho \(\Delta ABC\) có các đường cao \({\rm{BD}}\) và \({\rm{CE}}\) cắt nhau tại \({\rm{H}}\). Chứng minh:
a) \(\Delta HBE\) đồng dạng với \(\Delta HCD\).
b) \(\widehat {HDE} = \widehat {HAE}\).
Chứng minh các cặp tam giác đồng dạng, từ đó rút ra dữ kiện cần thiết để chứng minh yêu cầu của bài toán.
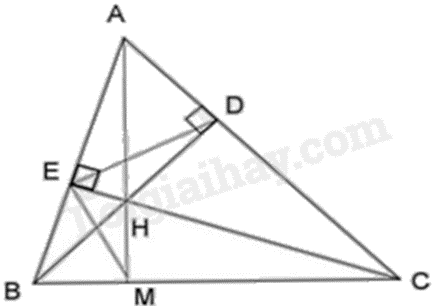
a) Xét \(\Delta HBE\) và \(\Delta HCD\) có:
\(\widehat {BDC} = \widehat {CEB} = {90^0}\)
\(\widehat {EHB} = \widehat {DHC}\) (2 góc đối đỉnh)
Suy ra $\Delta HBE\backsim \Delta HCD\left( g-g \right)$ (điều phải chứng minh)
b) Theo câu a) ta có: $\Delta HBE\backsim \Delta HCD$ suy ra \(\frac{{HE}}{{HD}} = \frac{{HB}}{{HC}}\) hay \(\frac{{HE}}{{HB}} = \frac{{HD}}{{HC}}\)
Xét \(\Delta HED\) và \(\Delta HBC\) ta có:
\(\frac{{HE}}{{HB}} = \frac{{HD}}{{HC}}\) (cmt)
\(\widehat {EHD} = \widehat {BHC}\) (hai góc đối đỉnh)
\(\widehat {HDE} = \widehat {HAE}\)
Suy ra $\Delta HED\backsim \Delta HBC\left( c-g-c \right).$
Mà đường cao \({\rm{BD}}\) và \({\rm{CE}}\) cắt nhau tại \({\rm{H}}\) (theo giả thiết)
Suy ra H là trực tâm của \(\Delta ABC\) hay \(AH \bot BC\) tại M suy ra \(\widehat {AMB} = {90^ \circ }\).
Xét \(\Delta AMB\) và \(\Delta CEB\) có:
\(\widehat {CEB} = \widehat {AMB} = {90^0}\)
\(\widehat B\) chung
Suy ra $\Delta AMB\backsim \Delta CEB\left( g-g \right)$
Suy ra \(\widehat {MAB} = \widehat {ECB}\) hay \(\widehat {HAE} = \widehat {HCB}\) (2)
Từ (1) và (2) ta có: \(\widehat {HDE} = \widehat {HAE}\) (điều phải chứng minh)

Các bài tập cùng chuyên đề
Một tàu du lịch đi từ Hải Phòng đến Quảng Ninh với quang đường dài \(50{\rm{\;km}}/{\rm{h}}\). Vận tốc của dòng nước là \(3{\rm{\;km}}/{\rm{h}}\). Gọi vận tốc thực của tàu là \(x{\rm{\;km}}/{\rm{h}}\). Hãy biểu diễn thời gian tàu đi ngược dòng từ Quảng Ninh tới Hải Phòng.
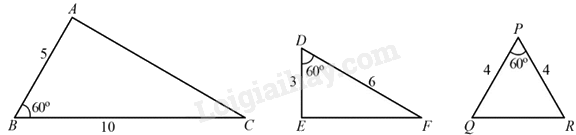
Quan sát hình sau và chỉ ra một cặp tam giác đồng dạng:
Đáp án nào dưới đây không là phương trình bậc nhất một ẩn?
Điều kiện xác định của phân thức \(\frac{{\left( {x - 1} \right)\left( {x + 3} \right)}}{{{x^2} - 1}}\) là:
Chọn khẳng định sai.
Hai tam giác nào không đồng dạng khi biết độ dài các cạnh của hai tam giác lần lượt là:
Kết quả của phép chia \(\frac{{a - 2b}}{{16}}:\frac{{2a - 4b}}{{12}}\) bằng:
Nếu 2 tam giác \({\rm{ABC}}\) và \({\rm{DEF}}\) có \(\widehat A = \widehat D,\widehat C = \widehat F\) thì:
Tổng các nghiệm của hai phương trình \( - 6\left( {1,5 - 2x} \right) = 3\left( { - 15 + 2x} \right);5x + 10 = 0\) bằng:
Cho biết một nửa đàn bò đang gặm cỏ trên cánh đồng, \(\frac{1}{3}\) đàn bò đang nằm nghỉ gần đó, còn lại 4 con đang uống nước ở ao. Tính số bò hiện có trong đàn.
Cho biểu thức: \(B = \frac{1}{{x + 1}} - \frac{{{x^3} - x}}{{{x^2} + 1}} \cdot \left( {\frac{1}{{{x^2} + 2x + 1}} - \frac{1}{{{x^2} - 1}}} \right)\) (ĐKXĐ: \(\left. {x \ne \pm 1} \right)\)
a) Rút gọn \(B\)
b) Tính giá trị của \(B\) tại \(x = - 2\)
c) Với giá trị nào của \(x\) thì \(B = 1\)
Giải các phương trình sau:
a) \(\frac{{9x + 5}}{6} = 1 - \frac{{6 + 3x}}{8}\);
b) \(\frac{{x + 1}}{4} = \frac{1}{2} + \frac{{2x + 1}}{5}\);
c) \(\frac{{2\left( {x + 1} \right)}}{3} = \frac{3}{2} - \frac{{1 - 2x}}{4}\).
Tổng số học sinh khối 8 và khối 9 của một trường là 580 em, trong đó có \(256\) em là học sinh giỏi. Tính số học sinh của mỗi khối, biết rằng số học sinh giỏi khối 8 chiếm tỉ lệ \(40{\rm{\% }}\) số học sinh khối 8, số học sinh giỏi khối 9 chiếm tỉ lệ 48% số học sinh khối 9.
Cho \(\frac{a}{{b + c}} + \frac{b}{{c + a}} + \frac{c}{{a + b}} = 1\). Chứng minh \(\frac{{{a^2}}}{{b + c}} + \frac{{{b^2}}}{{c + a}} + \frac{{{c^2}}}{{a + b}} = 0\)












