Nội dung từ Loigiaihay.Com
Cho tam giác ABC có AB = AC, N là trung điểm của BC.
a) Chứng minh \(\Delta ABN = \Delta ACN\).
b) Qua A kẻ đường thẳng a vuông góc với AN. Chứng minh a // BC.
c) Vẽ điểm F sao cho N là trung điểm của AF. Chứng minh AB + AC > 2AN.
a) Dựa vào các trường hợp bằng nhau của hai tam giác.
b) Chứng minh \(AN \bot BC\) suy ra a // BC.
c) Dựa vào bất đẳng thức tam giác để chứng minh.
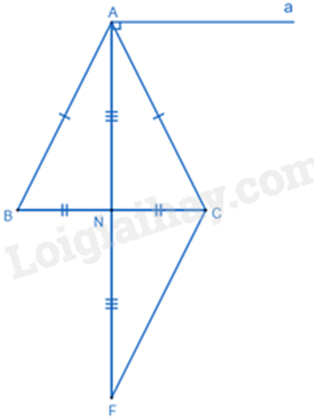
a) Xét \(\Delta ABN\) và \(\Delta ACN\) có:
\(\begin{array}{l}AB = AC(gt)\\BN = CN(gt)\\AN\,chung\end{array}\)
Suy ra \(\Delta ABN = \Delta ACN\)(c.c.c) (đpcm)
b) Ta có \(\Delta ABN = \Delta ACN\) suy ra \(\widehat {ANB} = \widehat {ANC}\).
Mà hai góc này là hai góc kề bù nên \(\widehat {ANB} = \widehat {ANC} = \frac{{{{180}^0}}}{2} = {90^0}\).
Do đó \(AN \bot BC\). Mà \(a \bot AN\) (gt)
Suy ra \(a//BC\) (từ vuông góc đến song song) (đpcm).
c) Xét \(\Delta ABN\) và \(\Delta FCN\) có:
\(\begin{array}{l}AN = NF(gt)\\BN = CN(gt)\end{array}\)
\(\widehat {ANB} = \widehat {FNC}\) (hai góc đối đỉnh)
Suy ra \(\Delta ABN = \Delta FCN\)(c.g.c) (đpcm)
Suy ra AB = CF.
Xét \(\Delta ACF\) có:
\(\begin{array}{l}CF + AC > AF\\AB + AC > 2AN\end{array}\)
(vì AB = CF và AF = 2AN) (đpcm).

Các bài tập cùng chuyên đề
Nếu 4.b = 5.c và b, c ≠ 0 thì:
Nếu các số x, y, z tỉ lệ với các số 6; 4; 3 thì ta có dãy tỉ số bằng nhau nào:
Đại lượng y tỉ lệ thuận với đại lượng x theo hệ số tỉ lệ 5. Ta có:
Cho x và y là hai đại lượng tỉ lệ thuận với nhau. Biết hệ số tỉ lệ của x đối với y là 8. Hệ số tỉ lệ của y đối với x là:
Cho biết y và x là hai đại lượng tỉ lệ nghịch theo hệ số tỉ lệ a. Ta có:
Cho tam giác ABC. Trong các khẳng định sau khẳng định nào sai?
Trong các biểu thức sau, em hãy chỉ ra biểu thức số.
Biểu thức biểu thị số tiền An phải trả để mua \(x\) quyển sách với giá \(10000\) đồng là:
Cho tam giác ABC có: \(\widehat A = {45^0};\widehat B = {60^0}\). So sánh các cạnh của tam giác ABC là:
Biểu thức nào là đa thức một biến?
Bậc của đa thức \({x^3} + 2{x^2} + 3x - 5\) là
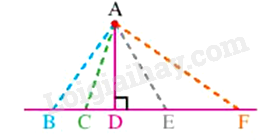
Cho hình vẽ, có bao nhiêu đường xiên kẻ từ điểm A đến đường thẳng BF?
1. Tìm x biết: \(\frac{x}{4} = \frac{7}{5}\).
2. Cho biết đại lượng x và y tỉ lệ thuận với nhau và khi x = 20 thì y = 12.
a) Tìm hệ số tỉ lệ của y đối với x và biểu diễn y theo x.
b) Tính giá trị của x khi \(y = \frac{{ - 1}}{3}\).
Ba lớp 7A, 7B, 7C thu tập tặng bạn vùng bão. Biết số vở của ba lớp lần lượt tỉ lệ với 3; 4; 5 và tổng số vở của lớp 7A và 7C là 240 cuốn. Tính số vở của mỗi lớp thu được.
Một đội công nhân có 15 người làm xong công việc trong 90 ngày. Hỏi cần bổ sung thêm bao nhiêu công nhân để hoàn thành công việc đó chỉ trong 50 ngày.
So sánh các cạnh của tam giác ABC có \(\widehat A = {50^0},\,\widehat B = {60^0}\).












