Nội dung từ Loigiaihay.Com
Cho d là đường trung trực của đoạn thẳng AB. Gọi O là trung điểm của AB. Trên d lấy 2 điểm M, N sao cho OM = ON. Tứ giác AMBN là hình gì? Chọn câu trả lời đúng nhất.
-
A.
Hình chữ nhật
-
B.
Hình vuông
-
C.
Hình thoi
-
D.
Hình bình hành
Sử dụng tính chất đường trung trực của đoạn thẳng.
Áp dụng các trường hợp bằng nhau của tam giác suy ra các cạnh bằng nhau.

Vì M nằm trên đường trung trực của AB nên MA = MB ( tính chất)
Vì N nằm trên đường trung trực của AB nên NA = NB ( tính chất)
Xét tam giác AOM và AON có:
OM = ON
\(\widehat {AOM} = \widehat {AON}( = 90^\circ )\)
AO chung
\( \Rightarrow \Delta AOM = \Delta AON\) ( c.g.c)
\( \Rightarrow \) AM = AN ( 2 cạnh tương ứng)
Mà MA = MB; NA = NB
\( \Rightarrow \) MA = MB = NB = NA
\( \Rightarrow \) Tứ giác AMBN là hình thoi ( Tứ giác có 4 cạnh bằng nhau)
Đáp án : C

Các bài tập cùng chuyên đề
Chọn câu sai.
Hai góc nhọn của tam giác vuông cân bằng nhau và bằng
Cho tam giác $ABC$ cân tại $A.$ Phát biểu nào trong các phát biểu sau là sai:
Một tam giác cân có góc ở đỉnh bằng \({64^0}\) thì số đo góc ở đáy là:
Một tam giác cân có góc ở đáy bằng \({70^0}\) thì số đo góc ở đỉnh là:
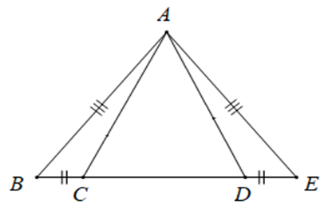
Số tam giác cân trong hình vẽ dưới đây là:
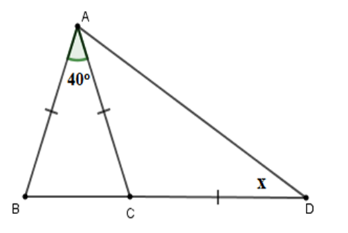
Tính số đo \(x\) trên hình vẽ sau:
Cho tam giác $ABC$ cân tại đỉnh $A$ với \(\widehat A = {80^0}\). Trên hai cạnh $AB,AC$ lần lượt lấy hai điểm $D$ và $E$ sao cho $AD = AE.$ Phát biểu nào sau đây là sai?
Cho tam giác \(ABC\) có \(\widehat A = 90^\circ ;\,AB = AC\). Khi đó
Cho tam giác \(ABC\) có \(M\) là trung điểm của \(BC\) và \(AM = \dfrac{{BC}}{2}\). Số đo góc \(BAC\) là
Tam giác \(ABC\) có \(\widehat A = 40^\circ ;\,\widehat B - \widehat C = 20^\circ .\) Trên tia đối của tia \(AC\) lấy điểm \(E\) sao cho \(AE = AB.\) Tính số đo góc \(CBE.\)
Cho tam giác \(ABC\) có \(\widehat A = 120^\circ .\) Trên tia phân giác của góc \(A\) lấy điểm \(D\) sao cho \(AD = AB + AC.\) Khi đó tam giác \(BCD\) là tam giác gì?
Cho tam giác $ABC$ có \(\widehat A = {60^ \circ }\). Vẽ ra phía ngoài của tam giác hai tam giác đều $AMB$ và $ANC.$
Để hai tam giác cân bằng nhau thì phải cần điều kiện là:
Cho tam giác ABC cân tại A. Phát biểu nào trong các phát biểu sau là sai:
Một tam giác cân có góc ở đỉnh bằng \({54^0}\) thì số đo góc ở đáy là:
Phát biểu nào sau đây là đúng:
Cho tam giác ABC cân tại B. Kẻ đường trung trực của BA cắt AB tại H, trung trực của BC cắt BC tại K và trung trực của AC cắt AC tại L. 3 đường trung trực này cắt nhau tại I.
Cho tam giác ABC cân tại đỉnh A với \(\widehat A = {80^0}\). Trên hai cạnh AB, AC lần lượt lấy hai điểm D và E sao cho AD = AE. Phát biểu nào sau đây là sai?
Cho tam giác ABC có \(\widehat A = {60^ \circ }\). Vẽ ra phía ngoài của tam giác hai tam giác đều AMB và ANC.
Khẳng định đúng là:












