Nội dung từ Loigiaihay.Com
Cho tam giác $ABC$ có \(\widehat A = {60^ \circ }\). Vẽ ra phía ngoài của tam giác hai tam giác đều $AMB$ và $ANC.$
-
A.
Ba điểm $M,A,N$ thẳng hàng.
-
B.
$BN = CM$
-
C.
Cả A, B đều sai
-
D.
Cả A, B đều đúng
+ Ta sử dụng tính chất tam giác cân, tính chất tia phân giác của một góc, tính chất hai góc kề bù để chứng minh các cặp góc so le trong bằng nhau để chứng minh ba điểm $M,A,N$ thẳng hàng.
+ Chứng minh cạnh bằng nhau ta sử dụng các trường hợp bằng nhau của tam giác để chứng minh hai tam giác bằng nhau từ đó suy ra hai cạnh tương ứng bằng nhau.
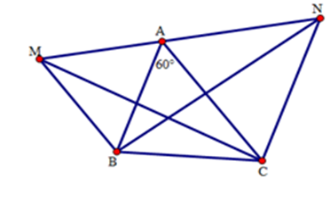
+ Các tam giác $AMB$ và $ANC$ là các tam giác đều(gt) nên \(\widehat {MAB} = {60^0},\,\,\,\widehat {NAC} = {60^0}\).
Ta có: \(\widehat {MAB} + \widehat {BAC} + \widehat {CAN} = {60^0} + {60^0} + {60^0} = {180^0}.\)
Suy ra ba điểm $M,A,N$ thẳng hàng.
+ Ta có:
$\widehat {MAC} = \widehat {MAB} + \widehat {BAC} = {60^0} + {60^0} = {120^0}\\\widehat {BAN} = \widehat {CAN} + \widehat {BAC} = {60^0} + {60^0} = {120^0}$
Do đó \(\widehat {MAC} = \widehat {BAN}\) .
Xét hai tam giác $ABN$ và $AMC$ có:
+) $AB = AM$ (do tam giác $AMB$ đều)
+) \(\widehat {BAN} = \widehat {MAC}\) (cmt)
+) $AN = AC$ (do tam giác $ANC$ đều)
Do đó \(\Delta ABN = \Delta AMC(c.g.c)\)
Suy ra $BN = CM$ (hai cạnh tương ứng).
Vậy cả A, B đều đúng.
Đáp án : D

Các bài tập cùng chuyên đề
Chọn câu sai.
Hai góc nhọn của tam giác vuông cân bằng nhau và bằng
Cho tam giác $ABC$ cân tại $A.$ Phát biểu nào trong các phát biểu sau là sai:
Một tam giác cân có góc ở đỉnh bằng \({64^0}\) thì số đo góc ở đáy là:
Một tam giác cân có góc ở đáy bằng \({70^0}\) thì số đo góc ở đỉnh là:
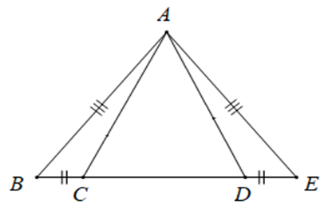
Số tam giác cân trong hình vẽ dưới đây là:
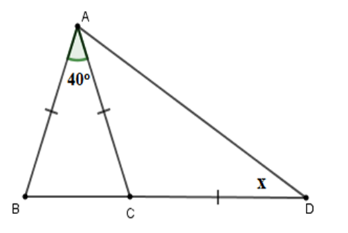
Tính số đo \(x\) trên hình vẽ sau:
Cho tam giác $ABC$ cân tại đỉnh $A$ với \(\widehat A = {80^0}\). Trên hai cạnh $AB,AC$ lần lượt lấy hai điểm $D$ và $E$ sao cho $AD = AE.$ Phát biểu nào sau đây là sai?
Cho tam giác \(ABC\) có \(\widehat A = 90^\circ ;\,AB = AC\). Khi đó
Cho tam giác \(ABC\) có \(M\) là trung điểm của \(BC\) và \(AM = \dfrac{{BC}}{2}\). Số đo góc \(BAC\) là
Tam giác \(ABC\) có \(\widehat A = 40^\circ ;\,\widehat B - \widehat C = 20^\circ .\) Trên tia đối của tia \(AC\) lấy điểm \(E\) sao cho \(AE = AB.\) Tính số đo góc \(CBE.\)
Cho tam giác \(ABC\) có \(\widehat A = 120^\circ .\) Trên tia phân giác của góc \(A\) lấy điểm \(D\) sao cho \(AD = AB + AC.\) Khi đó tam giác \(BCD\) là tam giác gì?
Cho \(M\) thuộc đoạn thẳng \(AB.\) Trên cùng một nửa mặt phẳng bờ \(AB,\) vẽ các tam giác đều \(AMC,BMD.\) Gọi \(E;F\) theo thứ tự là trung điểm của \(AD;BC.\) Tam giác \(MEF\) là tam giác gì? Chọn câu trả lời đúng nhất.
Cho tam giác \(ABC\) vuông tại \(A\) có \(\widehat B = {30^0}.\) Khi đó:
Cho tam giác \(ABC\) cân tại \(A\) có \(\widehat A = {120^0},BC = 6cm.\) Đường vuông góc với \(AB\) tại \(A\) cắt \(BC\) ở \(D.\) Độ dài \(BD\) bằng:
Cho tam giác \(ABC\) cân tại \(A\) có: \(\widehat A = {100^0}, BC = a, AC = b.\) Về phía ngoài tam giác \(ABC\) vẽ tam giác \(ABD\) cân tại \(D\) có: \(\widehat {ADB} = {140^0}.\) Tính chu vi tam giác \(ABD\) theo \(a\) và \(b.\)
Cho tam giác \(ABC\) cân tại \(B,\,\widehat {BAC} = {80^0}.\) Lấy \(I\) là điểm nằm trong tam giác sao cho \(\widehat {IAC} = {10^0};\widehat {ICA} = {30^0}.\) Tính góc \(ABI.\)












