Nội dung từ Loigiaihay.Com
Cho tam giác \(ABC\) có \(\widehat A = 120^\circ .\) Trên tia phân giác của góc \(A\) lấy điểm \(D\) sao cho \(AD = AB + AC.\) Khi đó tam giác \(BCD\) là tam giác gì?
-
A.
cân
-
B.
đều
-
C.
vuông
-
D.
vuông cân
Dựa vào tính chất tổng các góc của tam giác và dựa vào tính chất tam giác cân.
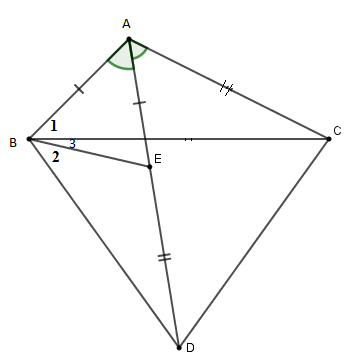
Lấy \(E \in AD\) sao cho \(AE = AB\) mà \(AD = AB + AC\) nên \(AC = DE.\)
\(\Delta ABE\) cân có \(\widehat {BAD} = 60^\circ \) nên \(\Delta ABE\) là tam giác đều suy ra \(AE = EB.\)
Thấy \(\widehat {BED} = \widehat {EBA} + \widehat {EAB} = 120^\circ \) (góc ngoài tại đỉnh \(E\) của tam giác \(ABE\) ) nên \(\widehat {BED} = \widehat {BAC}\left( { = 120^\circ } \right)\)
Suy ra \(\Delta EBD = \Delta {\rm A}BC\left( {c.g.c} \right) \Rightarrow \widehat {{B_1}} = \widehat {{B_2}}\) (hai góc tương ứng bằng nhau) và \(BD = BC\) (hai cạnh tương ứng)
Lại có $\widehat {{B_1}} + \widehat {{B_3}} = 60^\circ $ nên \(\widehat {{B_2}} + \widehat {{B_3}} = 60^\circ .\)
\(\Delta BCD\) cân tại \(B\) có \(\widehat {CBD} = 60^\circ \) nên nó là tam giác đều.
Đáp án : B

Các bài tập cùng chuyên đề
Chọn câu sai.
Hai góc nhọn của tam giác vuông cân bằng nhau và bằng
Cho tam giác $ABC$ cân tại $A.$ Phát biểu nào trong các phát biểu sau là sai:
Một tam giác cân có góc ở đỉnh bằng \({64^0}\) thì số đo góc ở đáy là:
Một tam giác cân có góc ở đáy bằng \({70^0}\) thì số đo góc ở đỉnh là:
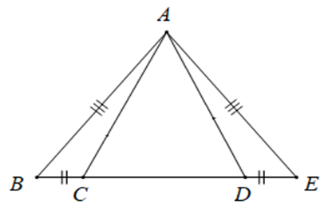
Số tam giác cân trong hình vẽ dưới đây là:
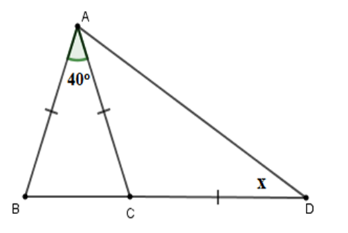
Tính số đo \(x\) trên hình vẽ sau:
Cho tam giác $ABC$ cân tại đỉnh $A$ với \(\widehat A = {80^0}\). Trên hai cạnh $AB,AC$ lần lượt lấy hai điểm $D$ và $E$ sao cho $AD = AE.$ Phát biểu nào sau đây là sai?
Cho tam giác \(ABC\) có \(\widehat A = 90^\circ ;\,AB = AC\). Khi đó
Cho tam giác \(ABC\) có \(M\) là trung điểm của \(BC\) và \(AM = \dfrac{{BC}}{2}\). Số đo góc \(BAC\) là
Tam giác \(ABC\) có \(\widehat A = 40^\circ ;\,\widehat B - \widehat C = 20^\circ .\) Trên tia đối của tia \(AC\) lấy điểm \(E\) sao cho \(AE = AB.\) Tính số đo góc \(CBE.\)
Cho tam giác $ABC$ có \(\widehat A = {60^ \circ }\). Vẽ ra phía ngoài của tam giác hai tam giác đều $AMB$ và $ANC.$
Cho \(M\) thuộc đoạn thẳng \(AB.\) Trên cùng một nửa mặt phẳng bờ \(AB,\) vẽ các tam giác đều \(AMC,BMD.\) Gọi \(E;F\) theo thứ tự là trung điểm của \(AD;BC.\) Tam giác \(MEF\) là tam giác gì? Chọn câu trả lời đúng nhất.
Cho tam giác \(ABC\) vuông tại \(A\) có \(\widehat B = {30^0}.\) Khi đó:
Cho tam giác \(ABC\) cân tại \(A\) có \(\widehat A = {120^0},BC = 6cm.\) Đường vuông góc với \(AB\) tại \(A\) cắt \(BC\) ở \(D.\) Độ dài \(BD\) bằng:
Cho tam giác \(ABC\) cân tại \(A\) có: \(\widehat A = {100^0}, BC = a, AC = b.\) Về phía ngoài tam giác \(ABC\) vẽ tam giác \(ABD\) cân tại \(D\) có: \(\widehat {ADB} = {140^0}.\) Tính chu vi tam giác \(ABD\) theo \(a\) và \(b.\)
Cho tam giác \(ABC\) cân tại \(B,\,\widehat {BAC} = {80^0}.\) Lấy \(I\) là điểm nằm trong tam giác sao cho \(\widehat {IAC} = {10^0};\widehat {ICA} = {30^0}.\) Tính góc \(ABI.\)












