Đề mẫu ĐGNL HN 2021

Hàm số $y = f\left( x \right)$ có đạo hàm $f'\left( x \right) = {x^3} - \dfrac{{29}}{8}{x^2} + \dfrac{9}{4}x + \dfrac{3}{8}$, $\forall x\, \in \,\mathbb{R}$. Gọi $S$ là tập hợp các điểm cực tiểu của hàm số $g\left( x \right) = f\left( {2x + 1} \right) - {x^3}.$ Tổng giá trị các phần tử của $S$ bằng

Cho hàm số $y = f\left( x \right)$ có đạo hàm trên $\left( {a;b} \right)$. Nếu $f'\left( x \right)$ đổi dấu từ âm sang dương qua điểm ${x_0}$ thuộc $(a;b)$ thì

Giả sử $y = f\left( x \right)$ có đạo hàm cấp hai trên $\left( {a;b} \right)$. Nếu $\left\{ \begin{gathered}f'\left( {{x_0}} \right) = 0 \hfill \\ f''\left( {{x_0}} \right) > 0 \hfill \\ \end{gathered}  \right.$ thì 

Nếu ${x_0}$ là điểm cực tiểu của hàm số thì $f\left( {{x_0}} \right)$ là:

Nếu ${x_0}$ là điểm cực đại của hàm số thì $\left( {{x_0};f\left( {{x_0}} \right)} \right)$ là:

Cho các phát biểu sau:

1. Hàm số $y = f\left( x \right)$ đạt cực đại tại ${x_0}$ khi và chỉ khi đạo hàm đổi dấu từ dương sang âm qua ${x_0}$.

2. Hàm số $y = f\left( x \right)$ đạt cực trị tại ${x_0}$ khi và chỉ khi ${x_0}$ là nghiệm của đạo hàm.

3. Nếu $f'\left( {{x_0}} \right) = 0$ và $f''\left( {{x_0}} \right) = 0$ thì ${x_0}$ không phải là cực trị của hàm số $y = f\left( x \right)$ đã cho.

4. Nếu $f'\left( {{x_0}} \right) = 0$ và $f''\left( {{x_o}} \right) > 0$ thì hàm số đạt cực đại tại ${x_0}$.

Các phát biểu đúng là:

Điều kiện để hàm số bậc ba không có cực trị là phương trình $y' = 0$ có:

Chọn phát biểu đúng:

Số điểm cực trị của đồ thị hàm số $y = \dfrac{{x - 1}}{{2 - x}}$ là:

Phương trình đường thẳng đi qua hai điểm cực trị của đồ thị hàm số $y = {x^3} - 3{x^2} + 1$ là:

Hàm số nào sau đây không có cực trị?

Hàm số $f\left( x \right) = 2\sin 2x - 3$ đạt cực tiểu tại:

Đồ thị hàm số nào sau đây có $3$ điểm cực trị?

Cho hàm số $y = f\left( x \right)$ có đạo hàm $f'\left( x \right) = \left( {x -1}\right)\left({{x^2}- 2} \right)\left( {{x^4} - 4} \right)$. Số điểm cực trị của hàm số $y = f\left( x \right)$ là:

Đồ thị hàm số $y = {x^3} - 3x + 2$ có $2$ điểm cực trị $A,\;B.$ Diện tích tam giác $OAB\;$ với $O(0;0)$ là gốc tọa độ bằng:

Cho hàm số $y = f\left( x \right)$ có bảng biến thiên trên khoảng $\left( {0;2} \right)$ như sau:

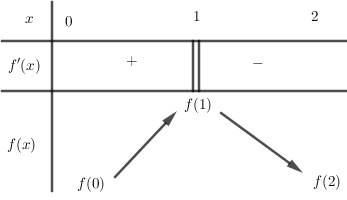
Khẳng định nào sau đây là khẳng định đúng:

Cho hàm số $y = f\left( x \right)$ có bảng biến thiên như sau:

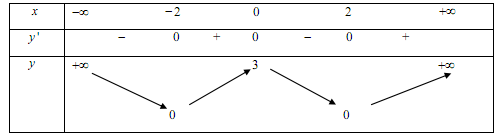
Khẳng định nào sau đây là khẳng định sai:

Cho hàm số $y = f\left( x \right)$ có bảng biến thiên như sau. Khẳng định nào dưới đây là đúng?

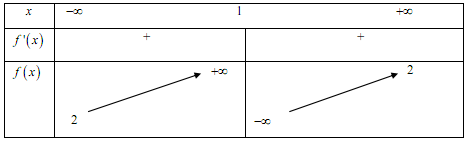
Cho hàm số $y = f\left( x \right)$ có bảng biến thiên như hình bên dưới, chọn khẳng định sai:

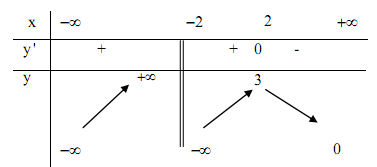
Hàm số $y = {x^3} - 3x^2 + 4$ đạt cực tiểu tại:

Cho hàm số $y = \dfrac{{ - {x^2} + 3x + 6}}{{x + 2}}$, chọn kết luận đúng: