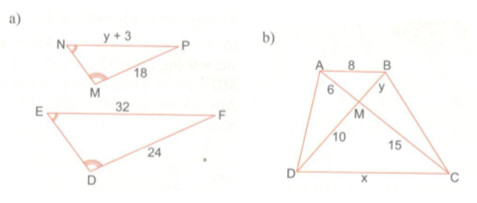
Bài tập 11 trang 90 Tài liệu dạy – học Toán 8 tập 2

Đề bài

a) Ở hình a, cho biết $\widehat N = \widehat E,\,\,\widehat M = \widehat D,\,\,MP = 18,\,\,$$DF = 24.$ Tính y

b) cho hình thang ABCD (hình b). Hãy điền vào chỗ trống:

$\Delta AMB \sim \Delta .....;$

${{AM} \over {.....}} = {{.....} \over {DC}} = {{MB} \over {.....}};\,\,x = ...;\,\,\,y = ...\,\,\,$

Lời giải chi tiết

a) Xét ∆MNP và ∆EDF có: $\widehat N = \widehat E(gt)$ và $\widehat M = \widehat D(gt)$

$\Rightarrow \Delta MNP \sim \Delta DEF(g.g)$

$\Rightarrow {{MP} \over {DF}} = {{NP} \over {EF}}$

$\Rightarrow {{18} \over {24}} = {{y + 3} \over {32}}$

$\Rightarrow {3 \over 4} = {{y + 3} \over {32}}$

$\Rightarrow 4(y + 3) = 96$

$\Rightarrow y + 3 = 24 \Rightarrow y = 21.$

b) • $\Delta AMB \sim \Delta CMD$ vì $\widehat {AMB} = \widehat {CMD}$ (hai góc đối đỉnh) và $\widehat {MAB} = \widehat {MCD}$ (hai góc so le trong và AB // CD)

• ${{AM} \over {CM}} = {{AB} \over {DC}} = {{MB} \over {MD}} \Rightarrow {6 \over {15}} = {8 \over x} = {y \over {10}}$

Từ đó suy ra:

$\eqalign{  & {6 \over {15}} = {8 \over x} \Rightarrow x = 20  \cr  & {6 \over {15}} = {y \over {10}} \Rightarrow y = 4 \cr}$

HocTot.Nam.Name.Vn