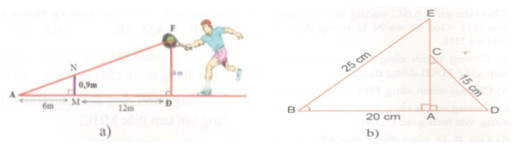
Bài tập 16 trang 91 Tài liệu dạy – học Toán 8 tập 2

Đề bài

a) Cho hai tam giác AMN và ADF có các kích thước như hình a. Tính DF.

b) Hình b, cho biết \(\widehat B = \widehat C,\,\,BE = 25\,cm,\,\,AB = 20cm,\)\(\,\,DC = 15cm.\) Tính CE.

Lời giải chi tiết

a) Xét ∆AMN và ∆ADF có: \(\widehat A\) (chung) và \(\widehat {NMA} = \widehat {FDA}( = 90^\circ )\)

\( \Rightarrow \Delta AMN \sim \Delta ADF(g.g)\)

\(\Rightarrow {{MN} \over {DF}} = {{AM} \over {AD}}\)

Mà \(MN = 0,9;AM = 6;\) \(AD = AM + MD = 18\) nên \({{0,9} \over {DF}} = {6 \over {18}} \Rightarrow DF = {{0,9.18} \over 6} = 2,7(m)\)

b) ∆ABE vuông tại A, ta có: \(A{E^2} + A{B^2} = B{E^2}\) (định lí Py-ta-go)

\( \Rightarrow A{E^2} + {20^2} = {25^2} \)

\(\Rightarrow A{E^2} = 225 \Rightarrow AE = 15(cm)\)

Xét ∆BAE và ∆CAD có: \(\widehat B = \widehat C(gt)\) và \(\widehat {BAE} = \widehat {CAD}( = 90^\circ )\)

\( \Rightarrow \Delta BAE \sim \Delta CAD(g.g)\)

\(\Rightarrow {{BA} \over {CA}} = {{BE} \over {CD}}\)

Nên \({{20} \over {CA}} = {{25} \over {15}} \Rightarrow CA = {{20.15} \over {25}} = 12(cm)\) và \(CE = AE - CA = 15 - 12 = 3(cm)\)

HocTot.Nam.Name.Vn