Đề thi THPT QG - 2021 - mã 101

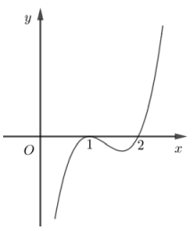
Cho hàm số \(y = f\left( x \right)\) có đồ thị là đường cong trong hình bên. Hàm số đã cho nghịch biến trên khoảng nào dưới đây?

Cho hàm số $y = f\left( x \right)$ đồng biến trên $D$ và ${x_1},{x_2} \in D$ mà ${x_1} > {x_2}$, khi đó:

Cho hàm số $f\left( x \right)$ xác định và có đạo hàm trên $\left( {a;b} \right)$. Nếu $f'\left( x \right) < 0,\forall x \in \left( {a;b} \right)$ thì:

Cho hàm số $y = f\left( x \right)$ nghịch biến và có đạo hàm trên $\left( { - 5;5} \right)$. Khi đó:

Hình dưới là đồ thị hàm số \(y = f'\left( x \right)\). Hỏi hàm số \(y = f\left( x \right)\) đồng biến trên khoảng nào dưới đây?

Cho hàm số \(y = f\left( x \right)\) xác định và liên tục trên \(\mathbb{R}\) và có đạo hàm \(f'\left( x \right) = {x^2} - 4\). Chọn khẳng định đúng:

Trong các hàm số dưới đây, hàm số nào không đồng biến trên $R?$

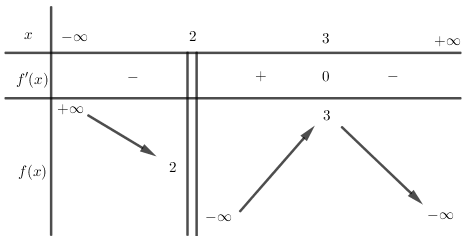
Cho hàm số $y = f\left( x \right)$ có bảng biến thiên như hình vẽ, chọn kết luận đúng:

Cho hàm số $y = f\left( x \right)$ xác định và có đạo hàm trên $\left( {a;b} \right)$. Chọn kết luận đúng:

Cho hàm số $y = f\left( x \right)$ xác định và có đạo hàm $f'\left( x \right) = 2{x^2}$ trên $R$. Chọn kết luận đúng:

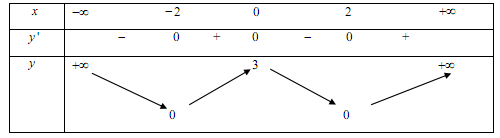
Cho hàm số $y = f\left( x \right)$ có bảng biến thiên như sau:

Khẳng định nào sau đây là khẳng định đúng:

Hàm số $y =  - {x^4} - 2{x^2} + 3$ nghịch biến trên:

Cho hàm số: $f(x) =  - 2{x^3} + 3{x^2} + 12x - 5.$ Trong các mệnh đề sau, tìm mệnh đề sai?

Hàm số $y = {x^3} - 3{{\rm{x}}^2} + 4$ đồng biến trên:

Trong tất cả các giá trị của tham số $m$ để hàm số $y = \dfrac{1}{3}{x^3} + m{x^2} - mx - m$ đồng biến trên $R$, giá trị nhỏ nhất của $m$ là:

Tìm các giá trị của tham số $m$ sao cho hàm số $y =  - {x^3} - {x^2} + mx + 1$ nghịch biến trên $R$?

Xác định giá trị của tham số $m$ để hàm số  $y = {x^3} - 3m{x^2} - m$ nghịch biến trên khoảng $\left( {0;1} \right)$.

Tìm $m$ để hàm số $y = \dfrac{{{x^3}}}{3} - 2m{x^2} + 4mx + 2$ nghịch biến trên khoảng $\left( { - 2;0} \right)$.

Tìm tất cả các giá trị thực của tham số $m$ để hàm số $y = \dfrac{{mx + 2}}{{2x + m}}$ nghịch biến trên từng khoảng xác định của nó?

Bất phương trình $\sqrt {2{x^3} + 3{x^2} + 6x + 16}  - \sqrt {4 - x}  \geqslant 2\sqrt 3 $ có tập nghiệm là $\left[ {a;b} \right].$ Hỏi tổng $a + b$ có giá trị là bao nhiêu?

Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đạo hàm \(f'\left( x \right) = {x^2}\left( {x - 2} \right)\left( {{x^2} - 6x + m} \right)\) với mọi \(x \in \mathbb{R}\). Có bao nhiêu số nguyên \(m\) thuộc đoạn \(\left[ { - 2019;\,2019} \right]\) để hàm số \(g\left( x \right) = f\left( {1 - x} \right)\) nghịch biến trên khoảng \(\left( { - \infty ;\, - 1} \right)\)?