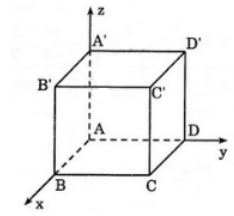
GIải bài 10 trang 81 SGK Hình học 12

LG a

a) Chứng minh rằng hai mặt phẳng \((AB'D')\) và \((BC'D)\) song song với nhau.

Phương pháp giải:

Chọn hệ trục tọa độ hợp lý sau đó suy ra tọa độ các điểm của hình lập phương.

+) Lập phương trình mặt phẳng \((AB'D')\) đi qua ba điểm \(A,\, \, B', \, D'\) có VTPT \(\overrightarrow{n_1} \) và mặt phẳng \((BC'D)\) đi qua ba điểm \(B,\, \, C', \, D\) có VTPT \(\overrightarrow{n_2} .\)

+) Chứng minh hai mặt phẳng này song song ta cần chứng minh \(\overrightarrow{n_1} \) cùng phương \(\overrightarrow{n_2}. \)

Lời giải chi tiết:

Chọn hệ trục tọa độ như hình vẽ có: \(O \equiv A,\;\;B \in Ox;\;D \in Oy,A'\in Oz.\)

Khi đó: \(A\left( {0;\;0;\;0} \right);\;\;B\left( {1;\;0;\;0} \right);\;C\left( {1;\;1;\;0} \right);\;D\left( {0;\;1;\;0} \right);\) \(A'\left( {0;\;0;\;1} \right);\;\;B'\left( {1;\;0;\;1} \right);\;C'\left( {1;\;1;1} \right);\;D'\left( {0;\;1;\;1} \right).\)

a) Ta có: \(\overrightarrow {AB'}  = \left( {1;\;0;\;1} \right);\overrightarrow {AD'}  = \left( {0;\;1;\;1} \right);\) \(\overrightarrow {BC'}  = \left( {0;\;1;\;1} \right);\) \(\overrightarrow {BD}  = \left( { - 1;\;1;\;0} \right).\)

Ta có: \( \left[{\overrightarrow {AB'} ,\overrightarrow {AD'} } \right]\) \( = \left( {\left| {\begin{array}{*{20}{c}}0&1\\1&1\end{array}} \right|;\;\left| {\begin{array}{*{20}{c}}1&1\\1&0\end{array}} \right|;\;\left| {\begin{array}{*{20}{c}}1&0\\0&1\end{array}} \right|} \right) \) \(= \left( { - 1; - 1;1} \right) =  - \left( {1;\;1;\; - 1} \right).\)

Mặt phẳng \((AB’D’)\) đi qua \(A\) và có VTPT \(\overrightarrow {{n_1}}=(1;1;-1)\) \(\Rightarrow\) Phương trình mặt phẳng \((AB’D’)\) là: \(x+y-z=0.\)

\(\overrightarrow {BC'}  = \left( {0;1;1} \right),\overrightarrow {DC'}  = \left( {1;0;1} \right)\)

\( \Rightarrow \left[ {\overrightarrow {BC'} ,\overrightarrow {DC'} } \right] = \left( {1;1; - 1} \right)\)

PT \(\left( {BC'D} \right):1\left( {x - 1} \right) + 1\left( {y - 0} \right) - 1\left( {z - 0} \right) = 0\) hay \(x+y-z-1=0.\)

Xét phương trình hai mặt phẳng ta có:

\(\dfrac{1}{1} = \dfrac{1}{1} = \dfrac{{ - 1}}{{ - 1}} \ne \dfrac{0}{{ - 1}} \) \(\Rightarrow \left( {AB'D'} \right)//\left( {BC'D} \right)\;\;\;\left( {dpcm} \right).\)

Chú ý : Bài này có thể làm không cần phương pháp tọa độ như sau:

Xét hai mặt phẳng \((AB'D')\) và \((BC'D)\), ta có \(BD // B'D'\) vì \(BB'D'D\) là hình chữ nhật, \(AD' // BC'\) vì \(ABC'D'\) là hình chữ nhật.

Do đó mặt phẳng \((AB'D')\) có hai đường thẳng cắt nhau \(B'D'\) và \(AD'\) lần lượt song song với hai đường thẳng cắt nhau \(BD\) và \(BC'\) của mặt phẳng \((BC'D)\). Vì vậy \((AB'D') // (BC'D)\)

LG b

b) Tính khoảng cách giữa hai mặt phẳng nói trên.

Phương pháp giải:

Hai mặt phẳng \((AB'D')\) và \((BC'D)\)  song song nên \(d((AB'D'),(BC'D) ) = d(A, (BC'D)).\)

+) Sử dụng công thức tính khoảng cách từ một điểm đến một mặt phẳng để tính.

Lời giải chi tiết:

Vì \((AB'D') // (BC'D)\) nên:

\(d((AB'D'),(BC'D) )=d(A,(BC'D))\) \( = \dfrac{{\left| {0 + 0 - 0 - 1} \right|}}{{\sqrt {{1^2} + {1^2} + {1^2}} }}=\dfrac{|-1|}{\sqrt{3}}=\dfrac{\sqrt{3}}{3}\)

HocTot.Nam.Name.Vn