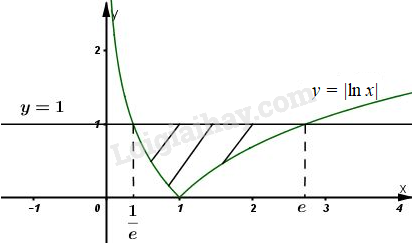
Giải bài 1 trang 121 SGK Giải tích 12

LG a

a) $y={x^2},y =x + 2$;   

Phương pháp giải:

Cho hai hàm số  $y = f\left( x \right);\;\;y = g\left( x \right)$ liên tục trên đoạn  $\left[ {a;\;b} \right]$. Gọi $D$ là hình phẳng được giới hạn bởi đồ thị hai hàm số trên và các đường thẳng  $x = a;\;\;x = b$. Khi đó diện tích của hình phẳng $D$ được tính bởi công thức: ${S_D} = \int\limits_a^b {\left| {f\left( x \right) - g\left( x \right)} \right|dx} .$

Lời giải chi tiết:

Phương trình hoành độ giao điểm của hai đồ thị là: $f(x) = x^2-x -2 =0$ $⇔(x+1)(x-2)=0$ $⇔\left[ \begin{array}{l}x + 1=0\\x - 2=0\end{array} \right.$ $⇔ \left[ \begin{array}{l}x = - 1\\x = 2\end{array} \right..$

Diện tích hình phẳng cần tìm là:

$S=\int_{-1}^{2}\left |x^{2}- x- 2 \right |dx$ $= \left | \int_{-1}^{2}\left (x^{2}- x- 2 \right ) dx \right |$

$=\left |\dfrac{x^{3}}{3}-\dfrac{x^{2}}{2}-2x|_{-1}^{2} \right |$ $=\left |\dfrac{8}{3}-2-4-(-\dfrac{1}{3}-\dfrac{1}{2}+2) \right |$ $=\dfrac{9}{2}$ (đvdt).

Quảng cáo

LG b

b) $y = |lnx|, y = 1$;

Lời giải chi tiết:

Phương trình hoành độ giao điểm của hai đồ thị là:

$f(x) = 1 - |\ln x| = 0  ⇔ \ln x = ± 1$ $⇔\left[ \begin{array}{l}x = e\\x =  \dfrac{1}{e}\end{array} \right..$ 

Ta có:  $y = |\ln x| = \ln x$  nếu  $\ln x ≥ 0$,  tức là  $x ≥ 1$.

hoặc  $y = |\ln x| = - \ln x$  nếu  $\ln x < 0$, tức là  $0 < x < 1$.

Dựa vào đồ thị hàm số vẽ ở hình trên ta có diện tích cần tìm là :  

$S=\int_{\frac{1}{e}}^{e}|1- |\ln x||dx$ $=\int_{\frac{1}{e}}^{1}(1+\ln x)dx$ $+\int_{1}^{e}(1-\ln x)dx$

$= x|_{\frac{1}{e}}^{1}+\int_{\frac{1}{e}}^{1}\ln xdx +x|_{1}^{e}-\int_{1}^{e}\ln xdx$

$= \left( {1 - \dfrac{1}{e}} \right) + \int\limits_{1/e}^1 {\ln xdx}$ $+ \left( {e - 1} \right) - \int\limits_1^e {\ln xdx}$

$=-\dfrac{1}{e}+e+\int_{\frac{1}{e}}^{1}\ln x dx-\int_{1}^{e}\ln xdx$

Tính $\int {\ln xdx}$ ta có:

Đặt $\left\{ \begin{array}{l}u = \ln x\\dv = dx\end{array} \right. \Rightarrow \left\{ \begin{array}{l}du = \dfrac{1}{x}dx\\v = x\end{array} \right.$

Do đó  $∫\ln xdx = x\ln x - ∫dx$ $= x\ln x  –  x  + C$, thay vào trên ta được:

$S=e-\dfrac{1}{e}+(x\ln x-x)|_{\frac{1}{e}}^{1}$ $- (x\ln x-x)|_{1}^{e}$ $= e - \dfrac{1}{e}$$+ \left[ {\left( {1\ln 1 - 1} \right) - \left( {\dfrac{1}{e}\ln \dfrac{1}{e} - \dfrac{1}{e}} \right)} \right]$  $- \left[ {\left( {e\ln e - e} \right) - \left( {1\ln 1 - 1} \right)} \right]$

$= e - \dfrac{1}{e}$$+ \left[ {\left( {0 - 1} \right) - \left( {\dfrac{1}{e}.\left( { - 1} \right) - \dfrac{1}{e}} \right)} \right]$  $- \left[ {\left( {e.1 - e} \right) - \left( {0 - 1} \right)} \right]$

$= e - \dfrac{1}{e} + \left( { - 1 + \dfrac{2}{e}} \right) - \left( {0 + 1} \right)$ $= e - \dfrac{1}{e} - 1 + \dfrac{2}{e} - 1$

$=e+\dfrac{1}{e}-2$ (đvdt).

LG c

c) $y = {\left( x-6 \right)}^2,y = 6x-{x^2}$ 

Lời giải chi tiết:

Phương trình hoành độ giao điểm của hai đồ thị là:

$f\left( x \right) =6x-{x^2}-{\left( {x -6} \right)^2}$ $= - 2({x^2}-9x+ 18)=0$

$\Leftrightarrow {x^2} - 9x + 18 = 0$ $⇔ (x-3)(x-6)=0$ $⇔ \left[ \begin{array}{l}x - 3=0\\x - 6=0\end{array} \right.$ $⇔\left[ \begin{array}{l}x = 3\\x = 6\end{array} \right..$

Diện tích cần tìm là:

$S=\int_{3}^{6}|-2(x^{2}-9x+18)|dx$ $=|2\int_{3}^{6}(x^{2}-9x+18)dx|$

$=\left |2(\dfrac{x^{3}}{3}-\dfrac{9}{2}x^{2}+18x)|_{3}^{6} \right |$

$= |2\left( {\dfrac{{{6^3}}}{3} - \dfrac{9}{2}{{.6}^2} + 18.6} \right)$ $- 2\left( {\dfrac{{{3^3}}}{3} - \dfrac{9}{2}{{.3}^2} + 18.3} \right)|$

$=|36-45|=9 \, \, (đvdt)$.

HocTot.Nam.Name.Vn