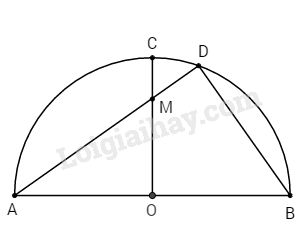
Bài 9 trang 87 Tài liệu dạy – học Toán 9 tập 1Giải bài tập Cho nửa đường tròn (O) có đường kính AB = 2R. Vẽ bán kính OC vuông góc với AB, gọi M là Đề bài Cho nửa đường tròn (O) có đường kính AB = 2R. Vẽ bán kính OC vuông góc với AB, gọi M là một điểm nằm trên OC sao cho tan^OAM=34, AM cắt nửa đường tròn tại D. Tính các đoạn AM, AD, BD theo R. Phương pháp giải - Xem chi tiết Sử dụng các tỉ số lượng giác, tỉ lệ đồng dạng và định lý Pythagore để tính. Lời giải chi tiết
Xét tam gác OAM vuông tại O có: tan^OAM=OMOA=34 ⇒OM=34OA=34R Áp dụng định lý Pythagore vào tam giác OAM vuông tại O: AM2=OA2+OM2 ⇒AM=√OA2+OM2=√R2+916R2=54R D là một điểm trên nửa đường tròn (O) ⇒^ADB=90o (góc nội tiếp chắn nửa đường tròn) Xét hai tam giác OAM và DAB có: +) ˆA chung; +) ^AOM=^ADB=90o ⇒Hai tam giác OAM và DAB đồng dạng ⇒AMAB=OAAD=OMBD⇒AD=OA.ABAM=R.2R54R=85RBD=OM.ABAM=34R.2R54R=65R HocTot.Nam.Name.Vn
|