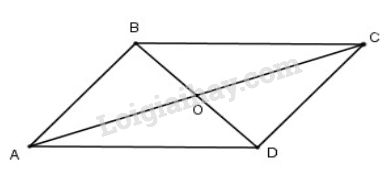
Bài 9 trang 59 SGK Hình học 10

Đề bài

Cho hình bình hành \(ABCD\) có \(AB = a, BC = b ,BD = m\), và \(AC = n\). Chứng minh rằng :

$${m^2} + {n^2} = 2({a^2} + {b^2})$$

Lời giải chi tiết

Gọi O là giao điểm của AC và BD. Khi đó O là trung điểm của AC và BD.

Tam giác ABD có AO là đường trung tuyến.

Áp dụng định lí về đường trung tuyến:

\(A{O^2} = \frac{{2\left( {A{B^2} + A{D^2}} \right) - B{D^2}}}{4}\)

Mà O là trung điểm AC nên \(AO = \frac{{AC}}{2} = \frac{n}{2}\)

Thay \(OA = \frac{n}{2}, \, AB = a,\) \(AD = BC = b\) và \(BD = m\) ta được: 

\(\begin{array}{l}
{\left( {\frac{n}{2}} \right)^2} = \frac{{2\left( {{a^2} + {b^2}} \right) - {m^2}}}{4}\\
\Leftrightarrow \frac{{{n^2}}}{4} = \frac{{2\left( {{a^2} + {b^2}} \right) - {m^2}}}{4}\\
\Leftrightarrow {n^2} = 2\left( {{a^2} + {b^2}} \right) - {m^2}\\
\Leftrightarrow {m^2} + {n^2} = 2\left( {{a^2} + {b^2}} \right)
\end{array}\)

Cách 2:

Áp dụng định lý đường trung tuyến cho tam giác ABC có BO là đường trung tuyến ra có:

\(\begin{array}{l}
B{O^2} = \frac{{2\left( {B{A^2} + B{C^2}} \right) - A{C^2}}}{4}\\
\Leftrightarrow {\left( {\frac{m}{2}} \right)^2} = \frac{{2\left( {{a^2} + {b^2}} \right) - {n^2}}}{4}\\
\Leftrightarrow \frac{{{m^2}}}{4} = \frac{{2\left( {{a^2} + {b^2}} \right) - {n^2}}}{4}\\
\Leftrightarrow {m^2} = 2\left( {{a^2} + {b^2}} \right) - {n^2}\\
\Leftrightarrow {m^2} + {n^2} = 2\left( {{a^2} + {b^2}} \right)
\end{array}\)

Cách 3:

Áp dụng định lí cô sin cho tam giác ABC có:

\(\begin{array}{l}
A{C^2} = A{B^2} + B{C^2} - 2AB.BC\cos \widehat {ABC}\\
\Rightarrow {n^2} = {a^2} + {b^2} - 2ab\cos \widehat {ABC}
\end{array}\)

Áp dụng định lí cô sin cho tam giác ABD có:

\(\begin{array}{l}
B{D^2} = A{B^2} + A{D^2} - 2AB.AD\cos \widehat {BAD}\\
\Rightarrow {m^2} = {a^2} + {b^2} - 2ab\cos \widehat {BAD}
\end{array}\)

\(\begin{array}{l}
\Rightarrow {m^2} + {n^2}\\
= \left( {{a^2} + {b^2}} \right) - 2ab\cos \widehat {ABC}\\
+ \left( {{a^2} + {b^2}} \right) - 2ab\cos \widehat {BAD}\\
= 2\left( {{a^2} + {b^2}} \right) - 2ab\left( {\cos \widehat {ABC} + \cos \widehat {BAD}} \right)
\end{array}\)

Mà \(\widehat {ABC} + \widehat {BAD} = {{180}^0} \) \( \Rightarrow \cos \widehat {ABC} =  - \cos \left( {{{180}^0} - \widehat {ABC}} \right) \) \(=  - \cos \widehat {BAD}\)

\( \Rightarrow \cos \widehat {ABC} + \cos \widehat {BAD} = 0\)

Vậy \({m^2} + {n^2} = 2\left( {{a^2} + {b^2}} \right)\).

HocTot.Nam.Name.Vn