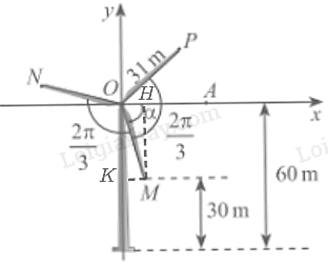
Bài 9 trang 24 SGK Toán 11 tập 1 - Chân trời sáng tạoTrong Hình 5, ba điểm M, N, P nằm ở đầu các cánh quạt của tua bin gió. Biết các cánh quạt dài 31m, độ cao của điểm M so với mặt đất là 30m, góc giữa các cánh quạt là (frac{{2pi }}{3})và số đo góc (OA, OM) là (alpha ). Tổng hợp đề thi học kì 2 lớp 11 tất cả các môn - Chân trời sáng tạo Toán - Văn - Anh - Lí - Hóa - Sinh Đề bài Trong Hình 5, ba điểm M, N, P nằm ở đầu các cánh quạt của tua bin gió. Biết các cánh quạt dài 31m, độ cao của điểm M so với mặt đất là 30m, góc giữa các cánh quạt là \(\frac{{2\pi }}{3}\) và số đo góc (OA, OM) là \(\alpha \). a) Tính sin\(\alpha \) và cos \(\alpha \). b) Tính sin của các góc lượng giác (OA, ON) và (OA, OP) từ đó tính chiều cao của các điểm N và P so với mặt đất (theo đơn vị mét). Làm tròn kết quả đến hàng phần trăm.  Phương pháp giải - Xem chi tiết Dựa vào hình vẽ để tìm sin\(\alpha \)và cos \(\alpha \); sử dụng công thức cộng để tính sin của các góc lượng giác (OA, ON) và (OA, OP). Lời giải chi tiết
a, Từ điểm M kẻ MH vuông góc với Ox, MK vuông góc với Oy. Ta có: MH = 60 – 30 = 30 m. Khi đó hoành độ điểm M là 30. ⇒ \(\;\sin \alpha {\rm{ }} = \;\frac{{MH}}{{OM}} = \;\frac{{30}}{{31}}\) \( \Rightarrow \cos \alpha = \sqrt {1 - {{\left( {\frac{{30}}{{31}}} \right)}^2}} = \frac{{\sqrt {61} }}{{31}}\) b, Vì các cánh quạt tạo thành 3 góc bằng nhau nên \(\widehat {MOP} = \widehat {NOP} = \widehat {MON} = {120^0}\) \( \Rightarrow \widehat {AOP} = \widehat {MOP} - \widehat {MOA}\) \( \Leftrightarrow \sin \widehat {AOP} = \sin \left( {\widehat {MOP} - \widehat {MOA}} \right) = \sin \widehat {MOP}.\cos \widehat {MOA} - \cos \widehat {MOP}.\sin \widehat {MOA}\) \( = \sin \frac{{2\pi }}{3}.\cos \alpha - \cos \frac{{2\pi }}{3}.\sin \alpha \approx 0,7\) Vì vậy chiều cao của điểm P so với mặt đất là: 31. \(\sin \widehat {AOP}\) + 60 = 31.0,7+ 60 \( \approx \) 81,76 m. Ta có: \(\cos \widehat {AOP} \approx \sqrt {1 - 0,{7^2}} = 0,71\) \(\widehat {AON} = \widehat {AOP} + \widehat {PON}\) \(\begin{array}{l} \Leftrightarrow \sin \widehat {AON} = \sin \left( {\widehat {AOP} + \widehat {PON}} \right)\\ \Leftrightarrow \sin \widehat {AON} = \sin \widehat {AOP}.\cos \widehat {PON} + \cos \widehat {AOP}.\sin \widehat {PON}\\ \Leftrightarrow \sin \widehat {AON} = 0,7.\cos \frac{{2\pi }}{3} + 0,71.\sin \frac{{2\pi }}{3} \approx 0,26\end{array}\) \( \Rightarrow \sin \left( {OA,ON} \right) = \sin \widehat {AON} \approx 0,26\) Vì vậy chiều cao của điểm N so với mặt đất là: 31. \(\sin \widehat {AON}\) + 60 = 31.0,26+ 60\( \approx \) 68,2 m.
|