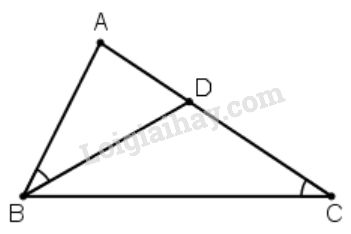
Bài 9 trang 132 SGK Toán 8 tập 2

Đề bài

Cho tam giác \(ABC\) có \(AB < AC\), \(D\) là một điểm nằm giữa \(A\) và \(C\). Chứng minh rằng : \(\widehat {ABD} = \widehat {ACB} \Leftrightarrow A{B^2} = AC.AD\)

Lời giải chi tiết

a) Chứng minh \(\widehat {ABD} = \widehat {ACB} \Rightarrow A{B^2} = AC.AD\)

Xét \(∆ABD\) và \(∆ACB\) có:

\(\widehat A\) chung (gt)

\(\widehat {ABD} = \widehat {ACB}\) (gt)

\(\Rightarrow \) \(∆ABD ∽ ∆ACB\) (g.g)

\( \Rightarrow \dfrac{{AB}}{{AC}} = \dfrac{{AD}}{{AB}} \Rightarrow A{B^2} = AC.AD\)

b) Chứng minh \(A{B^2} = AC.AD \Rightarrow  \widehat {ABD} = \widehat {ACB}\)

 \(A{B^2} = AC.AD\Rightarrow \dfrac{{AB}}{{AC}} = \dfrac{{AD}}{{AB}}\)

Xét \(∆ABD\) và \(∆ACB\) có:

\(\widehat A\) chung 

\(\dfrac{{AB}}{{AC}} = \dfrac{{AD}}{{AB}}\)

Suy ra \(∆ABD ∽ ∆ACB\) (c.g.c)

\(\Rightarrow \widehat {ABD} = \widehat {ACB}\) (Tính chất hai tam giác đồng dạng).

Vậy \(\widehat {ABD} = \widehat {ACB} \Leftrightarrow A{B^2} = AC.AD\)

HocTot.Nam.Name.Vn