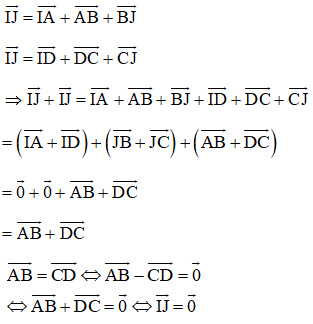Bài 9 trang 12 SGK Hình học 10

Đề bài

Chứng minh rằng \(\overrightarrow{AB}= \overrightarrow{CD}\) khi và chỉ khi trung điểm của hai đoạn thẳng \(AD\)  và \(BC\) trùng nhau.

Lời giải chi tiết

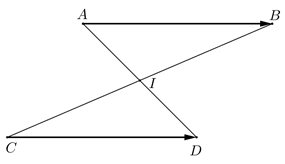
Ta chứng minh hai mệnh đề.

a) Cho \(\overrightarrow{AB}= \overrightarrow{CD}\) thì \(AD\) và \(BC\) có trung điểm trùng nhau.

Gọi \(I\) là trung điểm của \(AD\) ta chứng minh \(I\) cũng là trung điểm của \(BC\).

Theo quy tắc của ba điểm của tổng, ta có 

\(\overrightarrow{AB}= \overrightarrow{AI} + \overrightarrow{IB}\);

\(\overrightarrow{CD}= \overrightarrow{CI}+ \overrightarrow{ID}\)

Vì \(\overrightarrow{AB} = \overrightarrow{CD}\) nên \(\overrightarrow{AI} + \overrightarrow{IB}=  \overrightarrow{CI}+ \overrightarrow{ID}\)

\(\Rightarrow \overrightarrow{AI} - \overrightarrow{ID} = \overrightarrow{CI} - \overrightarrow{IB}\)

\(\Rightarrow\overrightarrow{AI} + \overrightarrow{DI} = \overrightarrow{CI} + \overrightarrow{BI}\)    (1)

Vì \(I\) là trung điểm của \(AD\) nên \(\overrightarrow {IA}  + \overrightarrow {ID}  = \overrightarrow 0  \Leftrightarrow \overrightarrow{AI} + \overrightarrow{DI} = \overrightarrow{0}\)  (2)

Từ (1) và (2) suy ra \(\overrightarrow{CI} + \overrightarrow{BI} = \overrightarrow{0} \Leftrightarrow \overrightarrow {IC}  + \overrightarrow {IB}  = \overrightarrow 0 \)  (3)

Đẳng thức (3) chứng tỏ \(I\) là trung điểm của \(BC\).

b) \(AD\) và \(BC\) có cùng trung điểm \(I\), ta chứng minh \(\overrightarrow{AB}\) = \(\overrightarrow{CD}\).

\(I\) là trung điểm của \(AD\) \( \Leftrightarrow \overrightarrow {IA}  + \overrightarrow {ID}  = \overrightarrow 0 \Rightarrow \overrightarrow{AI} + \overrightarrow{DI} = \overrightarrow{0}\)   \(\Rightarrow\overrightarrow{AI} - \overrightarrow{ID} =\overrightarrow{0}\)

\(I\) là trung điểm của \(BC\) \( \Leftrightarrow \overrightarrow {IC}  + \overrightarrow {IB}  = \overrightarrow 0 \) \(\Rightarrow \overrightarrow{CI} + \overrightarrow{BI}= \overrightarrow{0}\)    \(\Rightarrow \overrightarrow{CI} - \overrightarrow{IB}= \overrightarrow{0}\)

Suy ra  \(\overrightarrow{AI} - \overrightarrow{ID}=  \overrightarrow{CI}- \overrightarrow{IB}\) 

\(\Rightarrow \overrightarrow{AI} + \overrightarrow{IB} = \overrightarrow{CI}+ \overrightarrow{ID}\)    \(\Rightarrow \overrightarrow{AB}= \overrightarrow{CD}\) (đpcm)

Cách khác:

Gọi trung điểm của AD là I, trung điểm BC là J.

Khi đó ta có: \(\overrightarrow {IA}  + \overrightarrow {ID}  = \overrightarrow 0 ,\overrightarrow {JB}  + \overrightarrow {JC}  = \overrightarrow 0 \)

Mà theo quy tắc ba điểm ta có:

⇔ I ≡ J hay trung điểm AD và BC trùng nhau (đpcm).

HocTot.Nam.Name.Vn