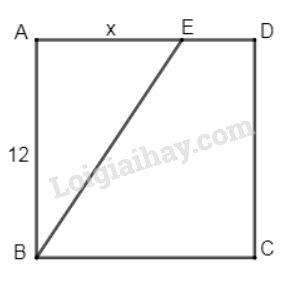
Bài 9 trang 119 SGK Toán 8 tập 1ABCD là một hình vuông cạnh 12cm. AE = x(cm) (h.123). Đề bài \(ABCD\) là một hình vuông cạnh \( 12cm\), \(AE = x(cm)\) (h.\(123\)). Tính \(x\) sao cho diện tích tam giác \(ABE\) bằng \(\dfrac{1}{3}\) diện tích hình vuông \(ABCD\).
Video hướng dẫn giải Phương pháp giải - Xem chi tiết Áp dụng: +) Công thức tính diện tích tam giác vuông: Diện tích tam giác vuông bằng nửa tích của hai cạnh góc vuông. +) Công thức tính diện tích hình vuông: Diện tích hình vuông bằng bình phương cạnh của nó. Lời giải chi tiết Diện tích tam giác vuông \(ABE\) là: \(S' = \dfrac{1}{2}AB.A{\rm{E}} = \dfrac{1}{2}.12.x = 6x\left( {c{m^2}} \right)\) Diện tích hình vuông là: \(S = 12.12 = 144\left( {c{m^2}} \right)\) Theo đề bài ta có: \(S' = \dfrac{S}{3}\) \(\Rightarrow 6x = \dfrac{{144}}{3} \) \(\Rightarrow 6x= 48\) \( \Rightarrow x = 48:6 = 8\left( {cm} \right)\). Vậy \(x = 8cm\). HocTot.Nam.Name.Vn  Chia sẻ Bình luận
Tham Gia Group Dành Cho 2K11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
