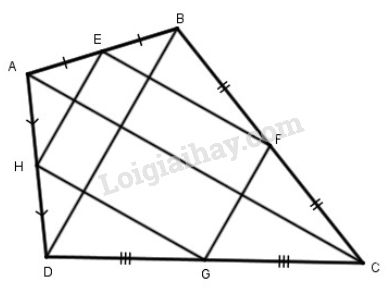
Bài 88 trang 111 SGK Toán 8 tập 1

Đề bài

Cho tứ giác $ABCD$. Gọi $E, F, G, H$ theo thứ tự là trung điểm của $AB, BC, CD, DA.$ Các đường chéo $AC, BD$ của tứ giác $ABCD$ có điều kiện gì thì $EFGH$ là:

a) Hình chữ nhật?

b) Hình thoi?      

c) Hình vuông

Lời giải chi tiết

+ Ta có: $EB = EA, FB = FC$ (gt)

Do đó $EF$ là đường trung bình của tam giác $ABC$

Suy ra $EF //AC, EF =  \dfrac{1}{2} AC$ (tính chất đường trung bình của tam giác)

+ Ta có: $HD = HA, GD = GC$ (gt)

Do đó $HG$ là đường trung bình của tam giác $ADC$

Suy ra $HG // AC, HG =  \dfrac{1}{2}AC$ (tính chất đường trung bình của tam giác)

Do đó $EF //HG, EF = HG$ nên $EFGH$ là hình bình hành.

+ Ta có: $EB = EA, AH = HD$ (gt)

Do đó $EH$ là đường trung bình của tam giác $ABD$.

Suy ra $EH //BD, EH =   \dfrac{1}{2}BD$ (tính chất đường trung bình của tam giác)

a) Hình bình hành $EFGH$ là hình chữ nhật $⇔EH  ⊥ EF$

$⇔ AC ⊥ BD$ (vì $EH // BD; EF // AC$)

Điều kiện phải tìm: các đường chéo $AC$ và $BD$ vuông góc với nhau.

b) Hình bình hành $EFGH$ là hình thoi $⇔ EF = EH$

  $⇔AC = BD$ (vì  $EF = \dfrac{1}{2}AC,EH = \dfrac{1}{2}BD)$

Điều kiện phải tìm: các đường chéo $AC$ và $BD$ bằng nhau.

c) Hình bình hành $EFGH$ là hình vuông khi và chỉ khi

$EFGH$ vừa là hình chữ nhật đồng thời là hình thoi.

$\Rightarrow AC ⊥ BD$ và $AC = BD$.

Điều kiện phải tìm: các đường chéo $AC, BD$ bằng nhau và vuông góc với nhau.

HocTot.Nam.Name.Vn