Bài 8 trang 117 Sách bài tập Hình học lớp 12 Nâng caoa)Cho hình hộp ABCD.A’B’C’D’ biết
Lựa chọn câu để xem lời giải nhanh hơn
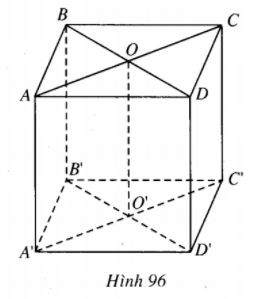
LG a Cho hình hộp ABCD.A’B’C’D’ biết \(A({x_1};{y_1};{z_1}),C({x_3};{y_3};{z_3}),B'(x{'_2};y{'_2};z{'_2}),\) \(D'(x{'_4};y{'_4};z{'_4}).\) Tìm tọa độ các đỉnh còn lại. Lời giải chi tiết:
Đặt \(O = AC \cap BD,O' = A'C' \cap B'D'.\) Ta có : \(\eqalign{ & O = \left( {{{{x_1} + {x_3}} \over 2};{{{y_1} + {y_3}} \over 2};{{{z_1} + {z_3}} \over 2}} \right), \cr & O' = \left( {{{x{'_2} + x{'_4}} \over 2};{{y{'_2} + y{'_4}} \over 2};{{z{'_2} + z{'_4}} \over 2}} \right) \cr} \) Từ \(\eqalign{ & \overrightarrow {AA'} = \overrightarrow {OO'} ,\overrightarrow {CC'} = \overrightarrow {OO'} , \cr & \overrightarrow {BB'} = \overrightarrow {OO'} ,\overrightarrow {{\rm{DD}}'} = \overrightarrow {OO'} \cr & \cr} \) Suy ra :
LG b Cho hình hộp ABCD.A’B’C’D’. Biết A(1;0;1), B(2;1;2), D(1;-1;1), C’(4;5;-5). Tìm tọa độ các đỉnh còn lại. Lời giải chi tiết: Ta có \(\overrightarrow {AC} = \overrightarrow {AB} + \overrightarrow {AD} \). Đặt C = (x;y;z), ta có : \(\left\{ \matrix{ x - 1 = (2 - 1) + (1 - 1) \hfill \cr y - 0 = (1 - 0) + ( - 1 - 0) \hfill \cr z - 1 = (2 - 1) + (1 - 1) \hfill \cr} \right. \Rightarrow \left\{ \matrix{ x = 2 \hfill \cr y = 0 \hfill \cr z = 2 \hfill \cr} \right. \) \(\Rightarrow C = (2;0;2).\) Mặt khác : \(\eqalign{ & \overrightarrow {AA'} = \overrightarrow {CC'} \Rightarrow A' = (3;5; - 6) \cr & \overrightarrow {BB'} = \overrightarrow {CC'} \Rightarrow B' = (4;6; - 5) \cr & \overrightarrow {{\rm{DD}}'} = \overrightarrow {CC'} \Rightarrow D' = (3;4; - 6). \cr} \) HocTot.Nam.Name.Vn
>> Lộ Trình Sun 2025 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi TN THPT & ĐGNL; ĐGTD - Click xem ngay) tại Tuyensinh247.com. Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, 3 bước chi tiết: Nền tảng lớp 12; Luyện thi chuyên sâu; Luyện đề đủ dạng đáp ứng mọi kì thi.
|