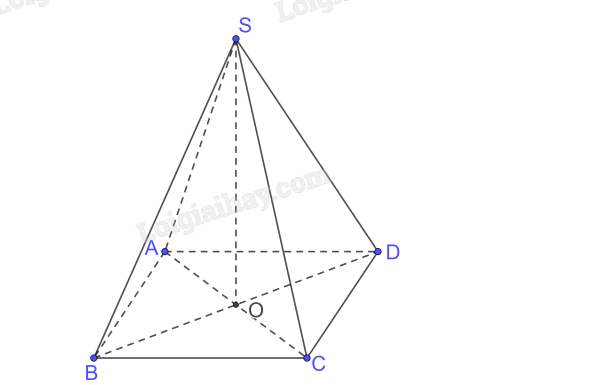
Bài 7.30 trang 63 SGK Toán 11 tập 2 - Kết nối tri thức

Đề bài

Cho khối chóp đều S.ABCD, đáy có cạnh 6 cm. Tính thể tích của khối chóp đó trong các trường hợp sau.

a) Cạnh bên tạo với mặt đáy một góc bằng ${60^0}.$

b) Mặt bên tạo với mặt đáy một góc bằng ${45^0}.$

Lời giải chi tiết

a)

 

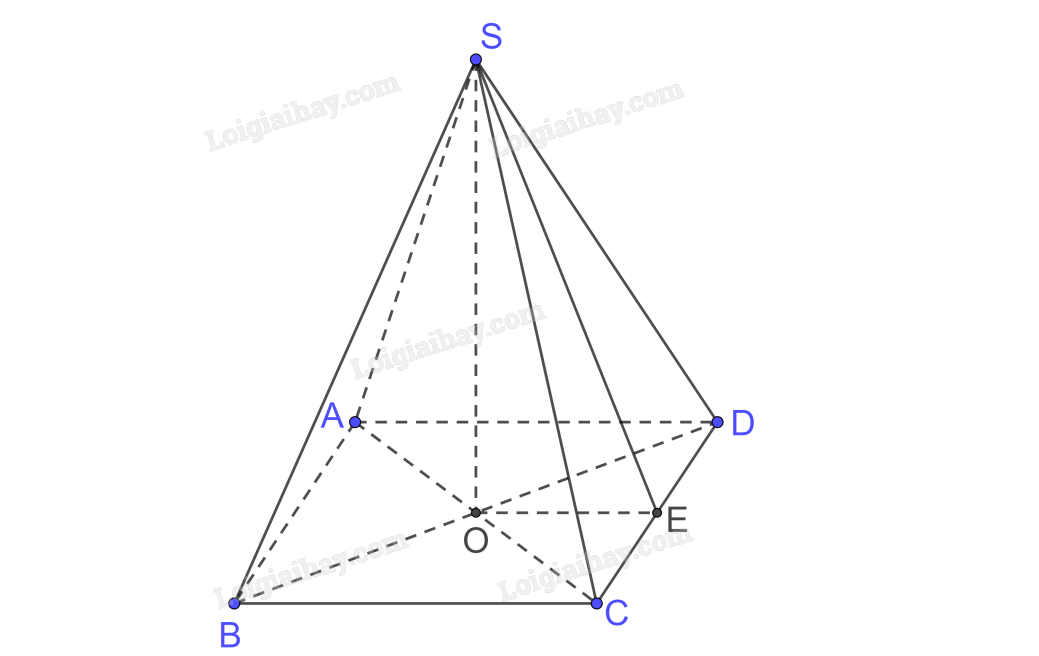
Gọi $AC \cap BD = \left\{ O \right\}$ mà S.ABCD đều nên $SO \bot \left( {ABCD} \right)$

$\Rightarrow$ O là hình chiếu của S trên (ABCD)

C là hình chiếu của C trên (ABCD)

$\Rightarrow$ OC là hình chiếu của SC trên (ABCD)

$\Rightarrow$ (SC, (ABCD)) = (SC, OC) $= \widehat {SCO}$

Mà cạnh bên tạo với mặt đáy một góc bằng ${60^0}.$

$\Rightarrow \widehat {SCO} = {60^0}$

Xét tam giác ABC vuông tại B có $AC = \sqrt {A{B^2} + B{C^2}}  = \sqrt {{6^2} + {6^2}}  = 6\sqrt 2 \left( {cm} \right)$

$\Rightarrow OC = \frac{{AC}}{2} = \frac{{6\sqrt 2 }}{2} = 3\sqrt 2 \left( {cm} \right)$

Xét tam giác SOC vuông tại O có

$\tan \widehat {SCO} = \frac{{SO}}{{OC}} \Rightarrow SO = 3\sqrt 2 .\tan {60^0} = 3\sqrt 6 \left( {cm} \right)$

${S_{ABCD}} = {6^2} = 36\left( {c{m^2}} \right)$

Vậy khối chóp có thể tích $V = \frac{1}{3}SO.{S_{ABCD}} = \frac{1}{3}.3\sqrt 6 .36 = 36\sqrt 6 \left( {c{m^3}} \right)$

b)

 

Trong (ABCD) kẻ $OE \bot CD$

$\begin{array}{l}SO \bot CD\left( {SO \bot \left( {ABCD} \right)} \right)\\ \Rightarrow CD \bot \left( {SOE} \right),SE \subset \left( {SOE} \right) \Rightarrow CD \bot SE,OE \bot CD,\left( {SCD} \right) \cap \left( {ABCD} \right) = CD\\ \Rightarrow \left( {\left( {SCD} \right),\left( {ABCD} \right)} \right) = \left( {SE,OE} \right) = \widehat {SEO}\end{array}$

Mà mặt bên tạo với mặt đáy một góc bằng ${45^0}.$

$\Rightarrow \widehat {SEO} = {45^0}$

Ta có $\left. \begin{array}{l}OE \bot CD\\AD \bot CD\end{array} \right\} \Rightarrow OE//AD$ mà O là trung điểm AC nên OE là đường trung bình tam giác ACD.

$\Rightarrow OE = \frac{{AD}}{2} = \frac{6}{2} = 3\left( {cm} \right)$

Xét tam giác SOE vuông tại O có

$\tan \widehat {SEO} = \frac{{SO}}{{OE}} \Rightarrow SO = 3.\tan {45^0} = 3\left( {cm} \right)$

Vậy khối chóp có thể tích $V = \frac{1}{3}SO.{S_{ABCD}} = \frac{1}{3}.3.36 = 36\left( {c{m^3}} \right)$