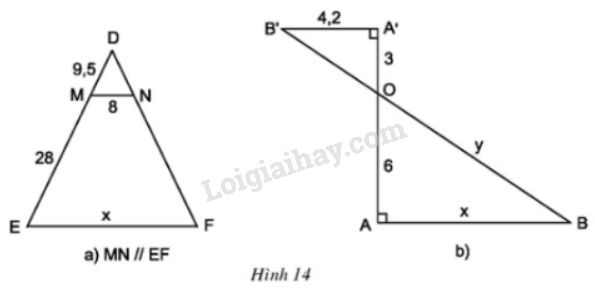
Bài 7 trang 62 SGK Toán 8 tập 2

Đề bài

 Tính các độ dài \(x,y\) trong hình 14.

Lời giải chi tiết

* Trong hình 14a

\(MN // EF\), theo hệ quả định lí Ta-lét ta có:

\( \dfrac{MN}{EF}=\dfrac{MD}{DE}\)

Mà \(DE = MD + ME = 9,5 + 28 = 37,5\).

\(\Rightarrow \dfrac{8}{x} = \dfrac{9,5}{37,5}\)

\(\Rightarrow x= \dfrac{8.37,5}{9,5}= \dfrac{600}{19}  ≈ 31,6\)

* Trong hình 14b

Ta có \(A'B' ⊥ AA'\) (giả thiết) và \(AB ⊥ AA'\) (giả thiết)

\( \Rightarrow  A'B' // AB\) (từ vuông góc đến song song)

\( \Rightarrow \dfrac{A'O}{OA} = \dfrac{A'B'}{AB}\) (Theo hệ quả định lí Ta-let)

hay \(\dfrac{3}{6} = \dfrac{4,2}{x}\)

\(x = \dfrac{6.4,2}{3} = 8,4\)

\(∆ABO\) vuông tại \(A\) nên áp dụng định lý Pitago ta có:

\(\eqalign{
& {y^2} = O{B^2} = O{A^2} + A{B^2} \cr
& \Rightarrow {y^2} = {6^2} + 8,{4^2} = 106,56 \cr
& \Rightarrow y = \sqrt {106,56} \approx 10,3 \cr} \)