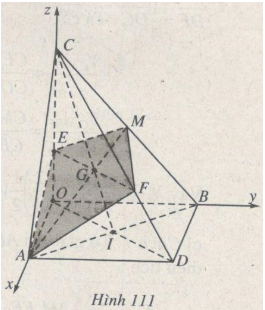
Bài 7 trang 224 Sách bài tập Hình học lớp 12 Nâng cao.

LG a

Gọi E là giao điểm của (P) với đường thẳng OC, tính độ dài đoạn thẳng OE.

Lời giải chi tiết:

(h.111)

Cách 1: Giả sử I là giao điểm của OD và AB, F là giao điểm củá mp(P) với CD. Khi đó dễ thấy ba đường thẳng EF, AM và CI đồng quy tại trọng tâm G của tam giác ABC.

Đặt $\overrightarrow {OE} {\rm{ }} = {\rm{ }}k.\overrightarrow {OC} .$

Từ giả thiết GA $\bot$ GE, ta có $\overrightarrow {GA} .\overrightarrow {GE}  = 0.$

Mặt khác $\overrightarrow {GA} .\overrightarrow {GE}  = \left( {\overrightarrow {OA}  - \overrightarrow {OG} } \right).\left( {\overrightarrow {OE}  - \overrightarrow {OG} } \right)$

$= \left[ {\overrightarrow {OA}  - {1 \over 3}\left( {\overrightarrow {OA}  + \overrightarrow {OB}  + \overrightarrow {OC} } \right)} \right].$

$\left[ {k\overrightarrow {OC}  - {1 \over 3}\left( {\overrightarrow {OA}  + \overrightarrow {OB}  + \overrightarrow {OC} } \right)} \right]$

$=  - {1 \over 3}\overrightarrow {O{A^2}}  + {1 \over 9}\overrightarrow {O{A^2}}  + {1 \over 9}\overrightarrow {O{B^2}}  + {1 \over 9}\overrightarrow {O{C^2}}  - {1 \over 3}k\overrightarrow {O{C^2}}$ (Vì $\overrightarrow {OA} .\overrightarrow {OB}  = \overrightarrow {OB} .\overrightarrow {OC}  = \overrightarrow {OC} .\overrightarrow {OA}  = 0$)

$=- {1 \over 3}{a^2} + {1 \over 9}{a^2} + {2 \over 9}{a^2} + {1 \over 9}{c^2} - {k \over 3}{c^2}$ (vì $OA = a,OB = a\sqrt 2 ,OC = c$).

Vậy $\overrightarrow {GA} .\overrightarrow {GE}  = 0 \Leftrightarrow {1 \over 9}{c^2} - {k \over 3}{c^2} = 0 \Leftrightarrow k = {1 \over 3}.$ Vậy $OE = {1 \over 3}c.$

Cách 2. Chọn hệ toạ độ Đề-các vuông góc Oxyz như hình 111 thì

$A{\rm{ }} = {\rm{ }}\left( {a{\rm{ }};{\rm{ }}0{\rm{ }};{\rm{ 0}}} \right),{\rm{ }}B{\rm{ }} = \left( {0;a\sqrt 2 ;0} \right){\rm{, }}D = {\rm{ }}\left( {a{\rm{ }};a\sqrt 2 ;{\rm{ }}0} \right),$

${\rm{ }}C = {\rm{ }}\left( {0{\rm{ }};{\rm{ }}0{\rm{ }};{\rm{ }}c} \right),$$M = \left( {0;{{a\sqrt 2 } \over 2};{c \over 2}} \right),$ Sử dụng giả thiết của bài toán, ta lập được phương trình của mặt phẳng (P) là $c\sqrt 2 \left( {x{\rm{ }} - a} \right) - {\rm{ }}cy{\rm{ }} + {\rm{ }}3a\sqrt 2 z{\rm{ }} = {\rm{ }}0$.

Giao điếm của (P) với trục Oz là $E{\rm{ }} = {\rm{ }}\left( {0{\rm{ }};{\rm{ }}0{\rm{ }};{c \over 3}} \right)$, suy ra $OE{\rm{ }} = {c \over 3}.$

LG b

Tính tỉ số thể tích của hai khối đa diện được tạo thành khi cắt khối chóp C.AOBD bởi mặt phẳng (P).

Lời giải chi tiết:

Vì $\overrightarrow {OE}  = {1 \over 3}\overrightarrow {OC}$ , giao tuyến EF của (P) với (OCD) song song với OD nên $\overrightarrow {DF}  = {1 \over 3}\overrightarrow {DC}$ . Ta có

$\eqalign{  & {{{V_{C.AEF}}} \over {{V_{C.AOD}}}} = {{CE} \over {CO}}.{{CF} \over {CD}} = {2 \over 3}.{2 \over 3} = {4 \over 9},  \cr  & {{{V_{C.MEF}}} \over {{V_{C.BOD}}}} = {{CM} \over {CB}}.{{CE} \over {CO}}.{{CF} \over {CD}} = {1 \over 2}.{2 \over 3}.{2 \over 3} = {2 \over 9}. \cr}$

Vậy ${V_{C.AEMF}} = \left( {{4 \over 9} + {2 \over 9}} \right){1 \over 2}{V_{C.AOBD}} = {1 \over 3}{V_{C.AOBD}}$, từ đó ${{{V_{C.AEMF}}} \over {{V_{AEMFDBO}}}} = {1 \over 2}.$

LG c

Tính khoảng cách từ điểm C đến mặt phẳng (P).

Lời giải chi tiết:

Cách 1. Tứ giác lồi AEMF có các đường chéo AM, EF vuông góc nên có diện tích :

${S_{AEMF}} = {1 \over 2}AM.FE$

$= {1 \over 2}\sqrt {A{O^2} + O{J^2} + J{M^2}} .{2 \over 3}OD$ (J là trung điểm của OB)

$= {1 \over 2}\sqrt {{a^2} + {{{a^2}} \over 2} + {{{c^2}} \over 4}} .{2 \over 3}\sqrt {{a^2} + 2{a^2}}  = {{\sqrt 3 } \over 6}a\sqrt {6{a^2} + {c^2}} .$

Vậy khoảng cách từ C đến mp(P) là

$d\left( {C{\rm{ }},{\rm{ }}\left( P \right)} \right) = {{3{V_{C.AEMF}}} \over {{S_{AEMF}}}} = {{{a^2}c{{\sqrt 2 } \over 3}} \over {{{\sqrt 3 } \over 6}a\sqrt {6{a^2} + {c^2}} }} = {{2ac\sqrt 6 } \over {3\sqrt {6{a^2} + {c^2}} }}.$

Cách 2. Sử dụng cách 2 của câu a), ta tính được khoảng cách từ điểm $C(0{\rm{ }};{\rm{ }}0{\rm{ }};c)$ đến mp(P) có phương trình $c\sqrt 2 \left( {x - a} \right) - cy{\rm{ }} + {\rm{ }}3a\sqrt 2 z{\rm{ }} = {\rm{ }}0$ là

$d\left( {C,\left( P \right)} \right) = {{\left| { - ac\sqrt 2  + 3ac\sqrt 2 } \right|} \over {\sqrt {2{c^2} + {c^2} + {\rm{ }}18{a^2}} }} = {{2ac\sqrt 6 } \over {3\sqrt {{c^2} + {\rm{ 6}}{a^2}} }}.$

HocTot.Nam.Name.Vn