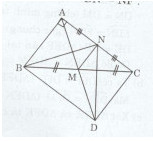
Bài 7 trang 176 Tài liệu dạy – học Toán 7 tập 1

Đề bài

Cho tam giác ABC vuông tại A. GỌi M là trung điểm của BC, trên tia đối của tia MA lấy điểm D sao cho M là trung điểm của AD.

a) Chứng minh rằng $\Delta MAB = \Delta MDC.$

b) Chứng minh rằng $CD \bot AC.$

c) Gọi N là trung điểm của AC. Chứng minh rằng NB = ND.

d) Cho $\widehat {ABC} = {60^0}.$  Chứng minh rằng $\Delta MAB$ đều. Tinh AC khi biết AB = 8 cm.

Lời giải chi tiết

a)Xét tam giác MAB và MDC có:

MA = MD (M là trung điểm của AD)

MB = MC (M là trung điểm của BC)

$\widehat {AMB} = \widehat {DMC}$   (hai góc đối đỉnh)

Do đó: $\Delta MAB = \Delta MDC(c.g.c).$

b) Ta có: $\widehat {ABM} = \widehat {DCM}(\Delta MAB = \Delta MDC)$

Mà góc ABM và DCM so le trong. Do đó: AB // CD.

Ta có: $AB \bot AC(\Delta ABC$  vuông tại A) và AB // CD (chứng minh trên) $\Rightarrow CD \bot AC.$

c) Xét tam giác ANB và CND ta có:

AN = CN (N là trung điểm của AC)

$\eqalign{  & \widehat {BAN} = \widehat {NCD}( = {90^0})  \cr  & AB = CD(\Delta MAB = \Delta MDC) \cr}$

Do đó: $\Delta ANB = \Delta CND(c.g.c) \Rightarrow NB = ND$

d) Xét tam giác ABC và CDA có:

AB = CD

$\widehat {BAC} = \widehat {DCA}( = {90^0})$

AC là cạnh chung.

Do đó: $\Delta ABC = \Delta CDA(c.g.c) \Rightarrow BC = AD$

Mà $MB = MC = {{BC} \over 2}$   (M là trung điểm của BC)

Và $MA = MD = {{AD} \over 2}$   (M là trung điểm của AD)

Do đó: MB = MC = MA = MD.

Tam giác MAB có MB = MA => tam giác MAB cân tại M

Mà $\widehat {ABC} = {60^0}(gt)$  . Do đó tam giác MAB đều => MB = AB = 8cm.

Ta có: BC = 2MB = 2.8 = 16 (cm)

Tam giác ABC vuông tại A

$\Rightarrow A{B^2} + A{C^2} = B{C^2}$   (định lí Pythagore)

Do đó: $A{C^2} = B{C^2} - A{B^2} = {16^2} - {8^2} = 256 - 64 = 192$

Mà AC > 0. Vậy $AC = \sqrt {192} (cm).$

HocTot.Nam.Name.Vn