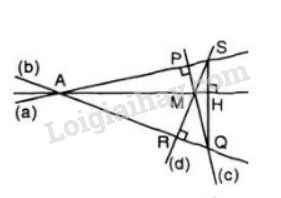
Bài 69 trang 88 SGK Toán 7 tập 2

Đề bài

Cho hai đường thẳng phân biệt không song song $a$ và $b$, điểm $M$ nằm bên trong hai đường thẳng này. Qua $M$ lần lượt vẽ đường thẳng $c$ vuông góc với $a$ tại $P$, cắt $b$ tại $Q$ và đường thẳng $d$ vuông góc với $b$ tại $R,$ cắt $a$ tại $S.$ Chứng minh rằng đường thẳng qua $M,$ vuông góc với $SQ$ cũng đi qua giao điểm của $a$ và $b.$

Lời giải chi tiết

Vì $a$ và $b$ không song song nên giả sử chúng cắt nhau tại $A.$

Xét $ΔAQS$ có:

    $QP ⊥ AS$ (vì $QP ⊥ a$) nên $QP$ là đường cao của tam giác $AQS$

    $SR ⊥ AQ$ (vì $SR ⊥ b$) nên $SR$ là đường cao của tam giác $AQS$

Ta có $QP$ và $RS$ cắt nhau tại $M.$ Vậy $M$ là trực tâm của $ΔAQS.$

$\Rightarrow$ Đường thẳng đi qua $M$ và vuông góc với $QS$ tại $H$ sẽ là đường cao thứ ba của $ΔAQS.$

Vậy $MH$ phải đi qua đỉnh $A$ của $ΔAQS$ hay đường thẳng vuông góc với $QS$ đi qua giao điểm của $a$ và $b$ (điều phải chứng minh).

HocTot.Nam.Name.Vn