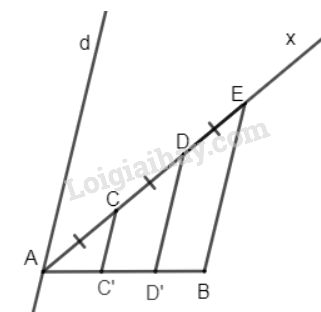
Bài 67 trang 102 SGK Toán 8 tập 1Cho đoạn thẳng AB. Kẻ tia Ax bất kì. Trên tia Ax Đề bài Cho đoạn thẳng \(AB\). Kẻ tia \(Ax\) bất kì. Trên tia \(Ax\) lấy các điểm \(C, D, E\) sao cho \(AC = CD = DE\) (h.97). Kẻ đoạn thẳng \(EB\). Qua \(C, D\) kẻ các đường thẳng song song với \(EB\). Chứng minh rằng đoạn thẳng \(AB\) bị chia ra ba phần bằng nhau. Video hướng dẫn giải Phương pháp giải - Xem chi tiết Áp dụng định lí: - Nếu các đường thẳng song song cách đều cắt một đường thẳng thì chúng chắn trên đường thẳng đó các đoạn thẳng liên tiếp bằng nhau. - Nếu các đường thẳng song song cắt một đường thẳng và chúng chắn trên đường thẳng đó các đoạn thẳng liên tiếp bằng nhau thì chúng song song cách đều. Lời giải chi tiết
Qua \(A\) dựng đường thẳng \(d\) song song với \(CC'\) Ta có: \(d//EB // DD' // CC'\) và \(AC = CD = DE\) (theo giả thiết). Theo định lí về các đường thẳng song song cách đều ta suy ra các đường thẳng \(d,EB,DD',CC'\) là các đường thẳng song song cách đều nên nó chắn trên \(AB\) các đoạn thẳng liên tiếp bằng nhau Hay \( AC' = C'D' = D'B\) Vậy đoạn thẳng \(AB\) bị chia thành ba phần bằng nhau. HocTot.Nam.Name.Vn  Chia sẻ Bình luận
Tham Gia Group Dành Cho 2K11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
