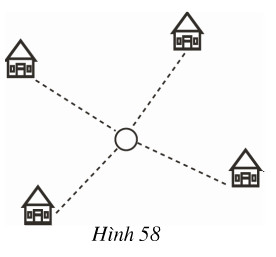
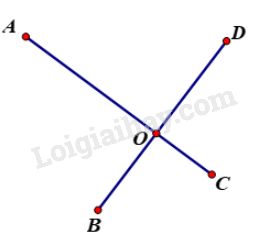
Bài 66 trang 87 SGK Toán 7 tập 2Đố: Bốn điểm dân cư được xây dựng như hình 58. Hãy tìm vị trí đặt một nhà máy sao cho tổng các khoảng cách từ nhà máy đến bốn điểm dân cư này là nhỏ nhất. Đề bài Đố: Bốn điểm dân cư được xây dựng như hình . Hãy tìm vị trí đặt một nhà máy sao cho tổng các khoảng cách từ nhà máy đến bốn điểm dân cư này là nhỏ nhất.
Video hướng dẫn giải Phương pháp giải - Xem chi tiết Áp dụng bất đẳng thức trong tam giác: Trong một tam giác, tổng độ dài hai cạnh bất kì bao giờ cũng lớn hơn độ dài cạnh còn lại. Lời giải chi tiết Gọi là nơi phải đặt nhà máy. lần lượt là bốn điểm dân cư. Tổng khoảng cách từ nhà máy đến khu dân cư là: Ta có: + Nếu nằm trên đoạn (và không trùng với giao điểm của và ) thì
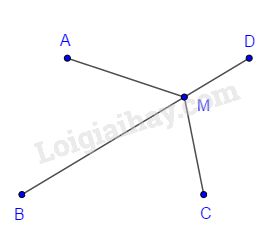
+ Nếu trùng với nằm trên đoạn (và không trùng với giao điểm của và (hình vẽ dưới)) thì
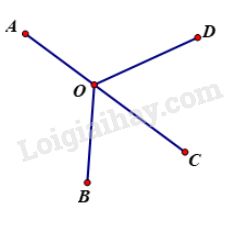
+ Nếu (trùng với ) không nằm trên và (hình vẽ dưới) thì theo bất đẳng thức tam giác ta có:
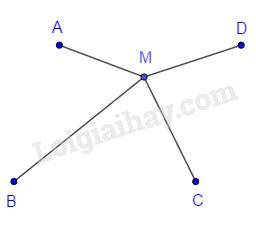
+ Nếu là giao điểm của và thì
- Vậy khi là giao điểm của và thì tổng khoảng cách từ nhà nhà máy này đến các khu dân cư là ngắn nhất. HocTot.Nam.Name.Vn
|