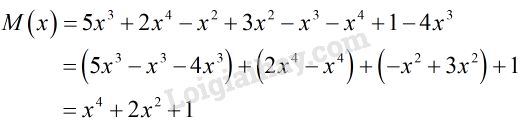Bài 63 trang 50 SGK Toán 7 tập 2Cho đa thức: Video hướng dẫn giải Cho đa thức: M(x)=5x3+2x4−x2+3x2−x3M(x)=5x3+2x4−x2+3x2−x3−x4+1−4x3−x4+1−4x3 LG a Sắp xếp các hạng tử của đa thức trên theo lũy thừa giảm của biến. Phương pháp giải: Thu gọn đa thức M(x)M(x) sau đó sắp xếp các hạng tử của đa thức trên theo lũy thừa giảm của biến. Lời giải chi tiết: Rút gọn:
Sắp xếp các hạng tử của đa thức M(x)M(x) theo lũy thừa giảm của biến: M(x)=x4+2x2+1M(x)=x4+2x2+1 LG b Tính M(1)M(1) và M(−1)M(−1) Phương pháp giải: Thay giá trị tương ứng của xx vào đa thức sau khi đã rút gọn rồi tính giá trị của đa thức đó. Lời giải chi tiết: Ta có: M(x)=x4+2x2+1M(x)=x4+2x2+1 Nên: M(1)=14+2.12+1=4M(1)=14+2.12+1=4 M(−1)=(−1)4+2.(−1)2+1=4M(−1)=(−1)4+2.(−1)2+1=4 LG c Chứng tỏ rằng đa thức trên không có nghiệm. Phương pháp giải: Đa thức không có nghiệm khi và chỉ khi đa thức đó luôn khác 00 với mọi xx. Lời giải chi tiết: Ta có: M(x)=x4+2x2+1M(x)=x4+2x2+1 Vì x4≥0x4≥0 với mọi x∈Rx∈R và x2≥0 với mọi x∈R ⇒M(x) không có nghiệm. HocTot.Nam.Name.Vn
|