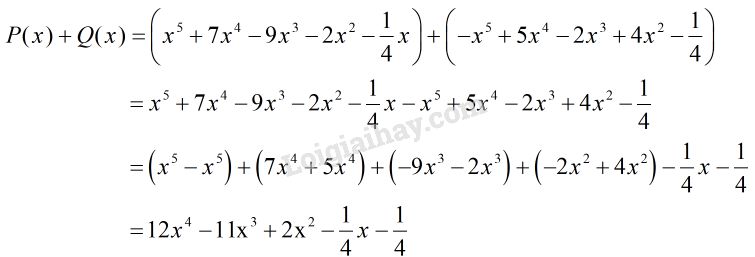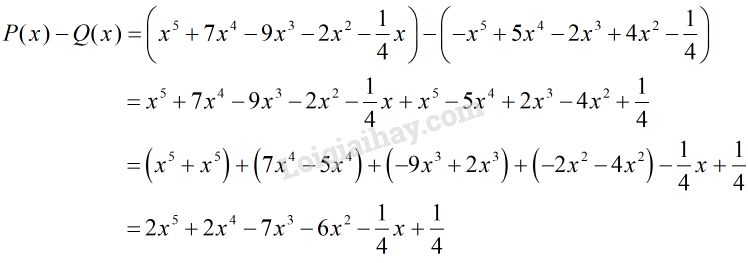Video hướng dẫn giải
VIDEO
Lựa chọn câu để xem lời giải nhanh hơn
Cho hai đa thức:
P ( x ) = x 5 − 3 x 2 + 7 x 4 − 9 x 3 + x 2 P ( x ) = x 5 − 3 x 2 + 7 x 4 − 9 x 3 + x 2 − 1 4 x − 1 4 x
Q ( x ) = 5 x 4 − x 5 + x 2 − 2 x 3 + 3 x 2 Q ( x ) = 5 x 4 − x 5 + x 2 − 2 x 3 + 3 x 2 − 1 4 − 1 4
LG a
Sắp xếp các hạng tử của mỗi đa thức trên theo lũy thừa giảm của biến.
Phương pháp giải:
Thu gọn và sắp xếp mỗi đa thức trên theo lũy thừa giảm của biến.
Lời giải chi tiết:
Ta có:
P ( x ) = x 5 − 3 x 2 + 7 x 4 − 9 x 3 + x 2 P ( x ) = x 5 − 3 x 2 + 7 x 4 − 9 x 3 + x 2 − 1 4 x − 1 4 x
= x 5 + 7 x 4 − 9 x 3 + ( − 3 x 2 + x 2 ) = x 5 + 7 x 4 − 9 x 3 + ( − 3 x 2 + x 2 ) − 1 4 x − 1 4 x
= x 5 + 7 x 4 − 9 x 3 − 2 x 2 − 1 4 x = x 5 + 7 x 4 − 9 x 3 − 2 x 2 − 1 4 x
Q ( x ) = 5 x 4 − x 5 + x 2 − 2 x 3 + 3 x 2 Q ( x ) = 5 x 4 − x 5 + x 2 − 2 x 3 + 3 x 2 − 1 4 − 1 4
= − x 5 + 5 x 4 − 2 x 3 + ( x 2 + 3 x 2 ) − 1 4 = − x 5 + 5 x 4 − 2 x 3 + ( x 2 + 3 x 2 ) − 1 4
= − x 5 + 5 x 4 − 2 x 3 + 4 x 2 − 1 4 = − x 5 + 5 x 4 − 2 x 3 + 4 x 2 − 1 4
LG b
Tính P ( x ) + Q ( x ) P ( x ) + Q ( x ) P ( x ) − Q ( x ) P ( x ) − Q ( x )
Phương pháp giải:
- Áp dụng qui tắc cộng, trừ đa thức một biến.
Lời giải chi tiết:
Cách khác:
LG c
Chứng tỏ rằng x = 0 x = 0 P ( x ) P ( x ) Q ( x ) Q ( x )
Phương pháp giải:
- Muốn kiểm tra một số a a f ( x ) f ( x )
- Tính f ( a ) = ? f ( a ) = ? f ( x ) f ( x ) x = a x = a
+) Nếu f ( a ) = 0 f ( a ) = 0 ⇒ ⇒ a a f ( x ) f ( x )
+) Nếu f ( a ) ≠ 0 f ( a ) ≠ 0 ⇒ ⇒ a a f ( x ) f ( x )
Lời giải chi tiết:
Ta có:
P ( x ) = x 5 + 7 x 4 − 9 x 3 − 2 x 2 − 1 4 x P ( x ) = x 5 + 7 x 4 − 9 x 3 − 2 x 2 − 1 4 x
Nên P ( 0 ) = 0 5 + 7.0 4 − 9.0 3 − 2.0 2 − 1 4 .0 P ( 0 ) = 0 5 + 7.0 4 − 9.0 3 − 2.0 2 − 1 4 .0 = 0 = 0
⇒ x = 0 ⇒ x = 0 P ( x ) P ( x )
Ta có: Q ( x ) = − x 5 + 5 x 4 − 2 x 3 + 4 x 2 − 1 4 Q ( x ) = − x 5 + 5 x 4 − 2 x 3 + 4 x 2 − 1 4
Nên Q ( 0 ) = − 0 5 + 5.0 4 − 2.0 3 + 4.0 2 − 1 4 Q ( 0 ) = − 0 5 + 5.0 4 − 2.0 3 + 4.0 2 − 1 4 = − 1 4 ≠ 0 = − 1 4 ≠ 0
⇒ x = 0 ⇒ x = 0 Q ( x ) Q ( x )
HocTot.Nam.Name.Vn