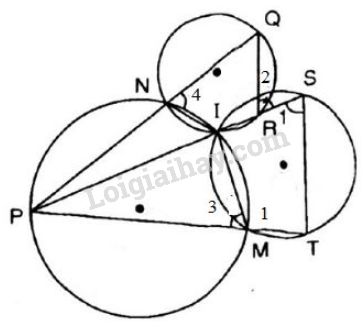
Bài 60 trang 90 SGK Toán 9 tập 2Xem hình 48. Chứng minh QR // ST. Đề bài Xem hình 48. Chứng minh \(QR // ST.\) Video hướng dẫn giải Phương pháp giải - Xem chi tiết + Sử dụng: Trong tứ giác nội tiếp tổng hai góc đối bằng \(180^0\) + Hai góc kề bù có tổng số đo bằng \(180^0\) + Chứng minh cặp góc so le trong \(\widehat{IST}= \widehat{SRQ}\) bằng nhau để suy ra hai đường thẳng song song. Lời giải chi tiết Kí hiệu như hình vẽ. +) Ta có tứ giác \(ISTM\) nội tiếp đường tròn nên: \(\widehat{S_{1}}+ \widehat{M_1}=180^0\) Mà \(\widehat{M_{1}}+ \widehat{M_{3}}= 180^0\) (2 góc kề bù) nên \(\widehat{S_{1}}= \widehat{M_{3}}\)(1) +) Ta có tứ giác \(IMPN\) nội tiếp đường tròn nên: \(\widehat{M_{3}}+ \widehat{PNI}=180^0\) Mà \(\widehat{N_{4}}+ \widehat{PNI}= 180^0\) (kề bù) nên \(\widehat{M_{3}}= \widehat{N_{4}}\) (2) +) Ta có tứ giác \(INQS\) nội tiếp đường tròn nên: \(\widehat{N_{4}}+ \widehat{IRQ}=180^0\) Mà \(\widehat{R_{2}}+ \widehat{IRQ}= 180^0\) (kề bù) nên \(\widehat{N_{4}}= \widehat{R_{2}}\) (3) Từ (1), (2), (3) suy ra \(\widehat{S_{1}}= \widehat{R_{2}}\) Mà hai góc này ở vị trí so le trong Do đó \(QR // ST.\)
|