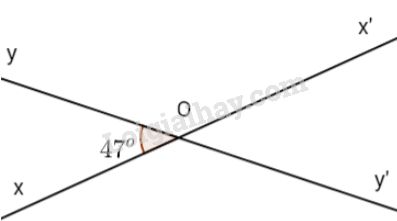
Bài 6 trang 83 SGK Toán 7 tập 1Vẽ hai đường thẳng cắt nhau sao cho trong các góc tạo thành có một góc 47^o. Tính số đo các góc còn lại. Đề bài Vẽ hai đường thẳng cắt nhau sao cho trong các góc tạo thành có một góc 47∘47∘. Tính số đo các góc còn lại. Video hướng dẫn giải Phương pháp giải - Xem chi tiết - Hai góc đối đỉnh thì bằng nhau - Tổng số đo hai góc kề bù bằng 180o180o. Lời giải chi tiết
Cách vẽ: Vẽ đường thẳng xx′. Lấy điểm O∈xx′, sau đó vẽ ^xOy=47∘. Vẽ tia Oy′ là tia đối của tia Oy. Khi đó ta được hình thỏa mãn bài toán. Ta có: ^xOy′+^xOy=180∘ (hai góc kề bù) ⇒^xOy′=180∘−^xOy=180∘−47∘=133∘ Ta có: Ox là tia đối của tia Ox′; Oy là tia đối của tia Oy′ suy ra ^x′Oy′ và ^xOy là hai góc đối đỉnh, ^x′Oy và ^xOy′ là hai góc đối đỉnh. Suy ra ^x′Oy′=^xOy=47∘ và ^x′Oy=^xOy′=133∘ Vậy ^x′Oy′=470,^x′Oy=^xOy′=133∘. HocTot.Nam.Name.Vn
|