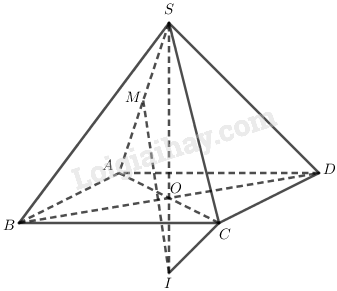
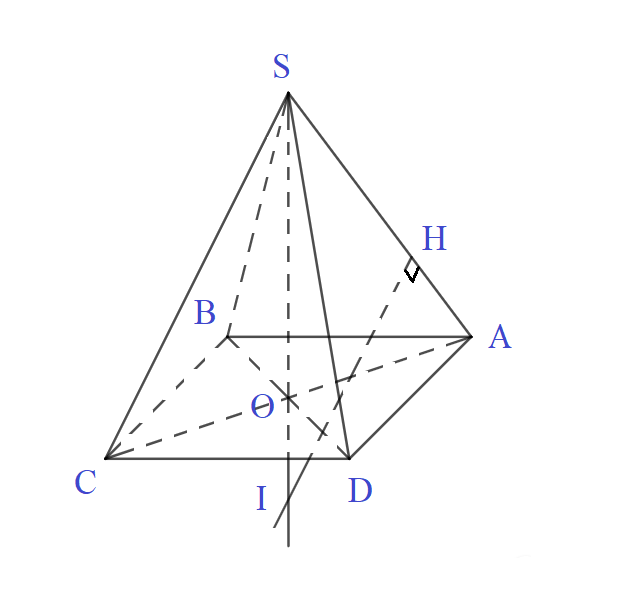
Bài 6 trang 50 SGK Hình học 12

Đề bài

Cho hình vuông $ABCD$ cạnh $a$. Từ tâm $O$ của hình vuông dựng đường thẳng $\Delta$ vuông góc với mặt phẳng $(ABCD)$. Trên $\Delta$ lấy điểm $S$ sao cho $OS ={a \over 2}$. Xác định tâm và bán kính mặt cầu ngoại tiếp hình chóp $S.ABCD$. Tính diện tích của mặt cầu và thể tích của khối cầu được tạo nên bởi mặt cầu đó.

Lời giải chi tiết

* Xác định mặt cầu ngoại tiếp

+ $\Delta$ là trục của mp đáy

Ta có $ABCD$ là hình vuông nên $O$ là tâm đường tròng ngoại tiếp hv $ABCD$ .

Lại có: $O \in \Delta ; \Delta \, \bot \, ABCD$ 

$\Rightarrow \Delta$ là trục của mp đáy

+ Xác định tâm $I$

Do $\Delta$ là trục của hình vuông $ABCD$, nên $I$ thuộc $\Delta$.

Ta có: $ABCD$ là hình vuông cạnh a $\Rightarrow AC = a\sqrt 2  \Rightarrow OC = \dfrac{1}{2}AC = \dfrac{{a\sqrt 2 }}{2}$

Mà $SO = \displaystyle {a \over 2} < OC$ nên $I$ thuộc phần kéo dài của tia $SO$.

+ Tìm bán kính $R$

Ta có: $SI = IC \Rightarrow \displaystyle {a \over 2} + OI = \sqrt {O{I^2} + O{C^2}}$

$\Rightarrow {\left( \displaystyle {{a \over 2} + OI} \right)^2} = O{I^2} +\displaystyle  {{{a^2}} \over 2}$

$\Rightarrow O{I^2} + a.OI + \displaystyle {{{a^2}} \over 4} = O{I^2} + \displaystyle {{{a^2}} \over 2}$

$\Rightarrow OI = \displaystyle {a \over 4} \Rightarrow R = SI = SO + OI = \displaystyle {{3a} \over 4}$

Vậy tâm $I$ của mặt cầu ngoại tiếp hình chóp $S.ABCD$ thuộc tia $SO$ mà $SI = R =$ $\displaystyle {{3a} \over 4}$ ; ($R$ là bán kính hình cầu).

Khi đó diện tích mặt cầu là: $S = 4\pi {R^2} = \displaystyle {9 \over 4}\pi {a^2}$ (đvdt)

Thể tích của khối cầu là: $V = \displaystyle {4 \over 3}\pi {R^3} = \displaystyle {9 \over {16}}{\pi a^3}$ (đvdt)

Cách khác:

Gọi $H$ là trung điểm cạnh $SA$

Trong  mặt phẳng $(SAO)$, đường trung trực của đoạn $SA$ cắt đường thẳng $SO$ tại $I$, ta có:

$\Delta SAO$ đồng dạng với $\Delta SIH$

$\Rightarrow \dfrac{{SA}}{{SO}} = \dfrac{{SI}}{{SH}} \Leftrightarrow SI = \dfrac{{SA.\,SH}}{{SO}} = \dfrac{{S{A^2}}}{{2\,SO}}$

Mà $S{A^2} = S{O^2} + O{A^2}$

$\begin{array}{*{20}{l}} { \Rightarrow S{A^2} = {{\left( {\dfrac{a}{2}} \right)}^2} + {{\left( {\dfrac{{a\sqrt 2 }}{2}} \right)}^2} = \dfrac{{3{a^2}}}{4}}\\ { \Rightarrow SA = \dfrac{{a\sqrt 3 }}{2}} \end{array}$

Khi đó: $SI = \frac{{\frac{{3{a^2}}}{4}}}{{2.\frac{a}{2}}} = \dfrac{{3a}}{4}$

Lại có: 

$\left. {\begin{array}{*{20}{l}} {IS = IA}\\ {IA = IB = IC = ID = \dfrac{{3a}}{4}} \end{array}} \right\} \Rightarrow IS = \dfrac{{3a}}{4}$

Vậy mặt cầu ngoại tiếp hình chóp $S.ABCD$ có tâm là $I$ và bán kính $R = IS = \dfrac{{3a}}{4}$

Diện tích mặt cầu là: $S = 4\pi {R^2} = 4\pi {\left( {\dfrac{{3a}}{4}} \right)^2} = \dfrac{{9\pi {a^2}}}{4}$

Thể tích khối cầu là: $V = \dfrac{4}{3}\pi {R^2} = \dfrac{4}{3}\pi {\left( {\dfrac{{3a}}{4}} \right)^3} = \dfrac{{9\pi {a^2}}}{{16}}$

 HocTot.Nam.Name.Vn