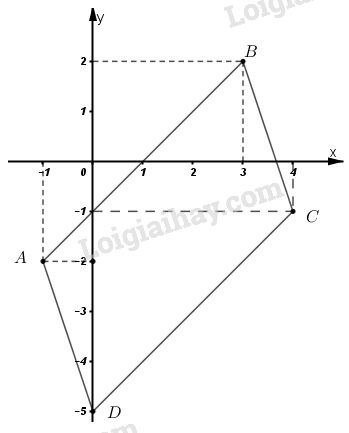
Bài 6 trang 27 (Hệ trục tọa độ) SGK Hình học 10Cho hình bình hành ABCD có A(-1; -2), B(3;2), C(4;-1). Tìm tọa độ điểm D. Đề bài Cho hình bình hành \(ABCD\) có \(A(-1; -2), B(3;2), C(4;-1)\). Tìm tọa độ điểm \(D.\) Video hướng dẫn giải Phương pháp giải - Xem chi tiết Dựa vào tính chất của hình bình hành: \(ABCD\) là hình bình hành \( \Leftrightarrow \overrightarrow {CD} = \overrightarrow {BA} \) Các công thức sử dụng: \(\overrightarrow {AB} = \left( {{x_B} - {x_A};{y_B} - {y_A}} \right)\) Hai véc tơ bằng nhau \(\overrightarrow u = \overrightarrow v \Leftrightarrow \left\{ \begin{array}{l} Lời giải chi tiết
Tứ giác \(ABCD\) là hình bình hành ⇔\(\overrightarrow{CD}=\overrightarrow{BA}\) Gọi \(D(x; y)\). Ta có: \(C(4;-1), D(x;y)\) nên \(\overrightarrow{CD} = (x-4; y+1)\) \(B(3;2), A(-1;-2)\) nên \(\overrightarrow{BA}= (-1-3;-2-2) = (-4;-4)\) \(\overrightarrow{CD}\) = \(\overrightarrow{BA}\) ⇔ \(\left\{\begin{matrix} x-4 = -4\\ y+1 = -4 \end{matrix}\right.\) \( \Leftrightarrow \left\{ \begin{array}{l} Vậy điểm \(D(0;-5)\) là điểm cần tìm. Chú ý: Ngoài điều kiện \( \Leftrightarrow \overrightarrow {CD} = \overrightarrow {BA} \) các em cũng có thể dùng \(\overrightarrow {AB} = \overrightarrow {DC} \) hoặc \(\overrightarrow {AD} = \overrightarrow {BC} \). HocTot.Nam.Name.Vn  Chia sẻ Bình luận
Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
