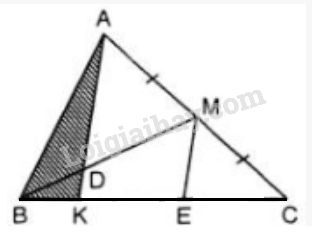
Bài 6 trang 132 SGK Toán 8 tập 2Cho tam giác ABC và đường trung tuyến BM. Trên đoạn thẳng BM lấy điểm D sao cho . Tia AD cắt BC ở K. Tìm tỉ số diện tích của tam giác ABK và tam giác ABC. Đề bài Cho tam giác \(ABC\) và đường trung tuyến \(BM\). Trên đoạn thẳng \(BM\) lấy điểm \(D\) sao cho \(\dfrac{{B{\rm{D}}}}{{DM}} = \dfrac{1}{2}\) . Tia \(AD\) cắt \(BC\) ở \(K\). Tìm tỉ số diện tích của tam giác \(ABK\) và tam giác \(ABC.\) Video hướng dẫn giải Phương pháp giải - Xem chi tiết Áp dụng: - Định lí: trong tam giác đường thẳng đi qua trung điểm của 1 cạnh và song song với cạnh thứ hai thì đi qua trung điểm của cạnh thứ 3. - Công thức tính diện tích tam giác. Lời giải chi tiết Kẻ \(ME\) song song với \(AK (E ∈ BC)\). Ta có: \(\dfrac{{BK}}{{KE}} = \dfrac{{BD}}{{DM}} = \dfrac{1}{2}\) \(\Rightarrow KE = 2BK\) Trong tam giác đường thẳng đi qua trung điểm của 1 cạnh và song song với cạnh thứ hai thì đi qua trung điểm của cạnh thứ 3. Do đó E là trung điểm cạnh KC. Suy ra \(ME\) là đường trung bình của tam giác \(ACK\) nên \(EC = KE = 2BK\). Ta có : \(BC = BK + KE + EC\)\(\, = BK + 2BK + 2BK = 5BK\) \( \Rightarrow \dfrac{{BK}}{{BC}} = \dfrac{1}{5}\) \(\dfrac{{{S_{ABK}}}}{{{S_{ABC}}}} = \dfrac{{BK}}{{BC}} = \dfrac{1}{5}\) (vì hai tam giác \(ABK\) và \(ABC\) có chung đường cao hạ từ \(A\)). HocTot.Nam.Name.Vn  Chia sẻ Bình luận
Tham Gia Group Dành Cho 2K11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
