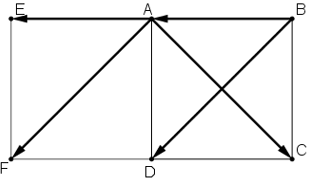
Bài 6 trang 40 SGK Hình học 10

Đề bài

Cho hình vuông $ABCD$. Tính: $\cos \left( {\overrightarrow {AC} ,\overrightarrow {BA} } \right), \, \sin\left( {\overrightarrow {AC} ,\overrightarrow {BD} } \right),$$\cos \left( {\overrightarrow {AB} ,\overrightarrow {CD} } \right).$

Lời giải chi tiết

+) Dựng $\overrightarrow {AE}  = \overrightarrow {BA}$ ta có :

$\left( {\overrightarrow {AC} ,\overrightarrow {BA} } \right) = \left( {\overrightarrow {AC} ,\overrightarrow {AE} } \right) = \widehat {CAE}$

Mà ABCD là hình vuông nên $\widehat {BAC} = {45^0}$

$\Rightarrow \widehat {CAE} = {180^0} - \widehat {BAC}$ $= {180^0} - {45^0} = {135^0}$

$\begin{array}{l} \Rightarrow \cos \left( {\overrightarrow {AC} ,\overrightarrow {BA} } \right) = \cos {135^0}\\ =  \cos \left( {{{180}^0} - {{45}^0}} \right) = - \cos {45^0}\\ = - \frac{1}{{\sqrt 2 }} \end{array}$

Vậy $\cos \left( {\overrightarrow {AC} ,\overrightarrow {BA} } \right) = -\frac{1}{{\sqrt 2 }}$

+) Dựng $\overrightarrow {AF}  = \overrightarrow {BD}$ ta có: $\left( {\overrightarrow {AC} ,\overrightarrow {BD} } \right) = \left( {\overrightarrow {AC} ,\overrightarrow {AF} } \right) = \widehat {CAF}$

Mà $\overrightarrow {AF}  = \overrightarrow {BD}$ nên AF//BD.

Lại có AC $\bot$ BD nên AC $\bot$ AF hay $\widehat {CAF}=90^0$.

Vậy $\cos \left( {\overrightarrow {AC} ,\overrightarrow {BD} } \right)$ $= \cos \widehat {CAF} = \cos {90^0} = 0$

+) Vì $\overrightarrow {AB} ,\overrightarrow {CD}$ là hai véc tơ ngược hướng nên:

$\left( {\overrightarrow {AB} ,\overrightarrow {CD} } \right) = {180^0}$ $\Rightarrow \cos \left( {\overrightarrow {AB} ,\overrightarrow {CD} } \right) = \cos {180^0} =  - 1$

HocTot.Nam.Name.Vn