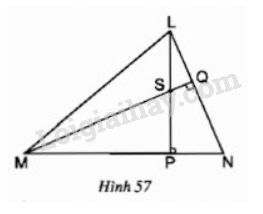
Bài 59 trang 83 SGK Toán 7 tập 2

Đề bài

Cho hình $57$.

 

a) Chứng minh $NS ⊥ LM$

b) Khi $\widehat{LNP} ={50^0}$, hãy tính góc $MSP$ và góc $PSQ.$

Lời giải chi tiết

a)  Trong $∆NML$ có : 

$LP ⊥ MN$ nên $LP$ là đường cao

$MQ ⊥ NL$ nên $MQ$ là đường cao

Mà $PL$ cắt $MQ$ tại $S$

Suy ra $S$ là trực tâm của tam giác $NML$ 

Do đó đường thằng $NS$ là đường cao kẻ từ $N$ của tam giác $NML$ hay $NS ⊥ LM.$

b) $∆NMQ$ vuông tại $Q$ và $\widehat{LNP} ={50^0}$ nên theo định lí tổng ba góc trong của một tam giác ta có:

$\eqalign{ & \widehat {QMN} = {180^o} - \left( {\widehat {MQN} + \widehat {QNM}} \right) \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\; = {180^o} - \left( {{{90}^o} + {{50}^o}} \right) = {40^0} \cr}$

$∆MPS$ vuông tại $P$ có $\widehat{QMP} ={40^0}$ nên theo định lí tổng ba góc trong của một tam giác ta có:

$\eqalign{ & \widehat {MSP} = {180^o} - \left( {\widehat {MPS} + \widehat {SMP}} \right) \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \;= {180^o} - \left( {{{90}^o} + {{40}^o}} \right) = {50^0} \cr}$

Ta có: $\widehat{MSP} +  \widehat{PSQ} = {180^0}$ ($2$ góc kề bù)

$\Rightarrow  \widehat{PSQ}  ={180^0}-\widehat{MSP}$$\,= {180^{0}} - {50^0} = {130^0}$

HocTot.Nam.Name.Vn