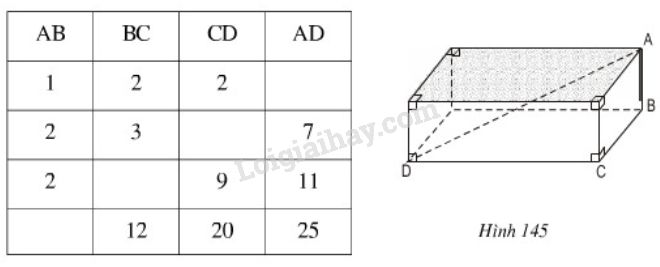
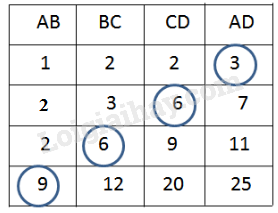
Bài 55 trang 128 SGK Toán 8 tập 2

Đề bài

\(A, B, C, D\) là các đỉnh của một hình hộp chữ nhật. Hãy quan sát hình 145 rồi điền số thích hợp vào các ô trống ở bảng sau:

 

Lời giải chi tiết

 Ở hàng (2):\(AD = \sqrt {A{B^2} + B{C^2} + C{D^2}}\)

\( = \sqrt {{1^2} + {2^2} + {2^2}}  = \sqrt 9  = 3\)

Ở hàng (3):\(BD = \sqrt {A{D^2} - A{B^2}}  = \sqrt {{7^2} - {2^2}}  \) \(= \sqrt {45} \)

 \(CD = \sqrt {B{D^2} - B{C^2}}  = \sqrt {45 - {3^2}}\) \(  = \sqrt {36}  = 6\)

Ở hàng (4):\(BD = \sqrt {A{D^2} - A{B^2}}  = \sqrt {{{11}^2} - {2^2}}  \) \(= \sqrt {117} \)

 \(BC = \sqrt {B{D^2} - D{C^2}}\)

\( = \sqrt {117 - {9^2}}  = \sqrt {117 - 81}  \)\(\,= \sqrt {36}  = 6\)

Ở hàng (5):\(BD = \sqrt {D{C^2} + B{C^2}}\)

\( = \sqrt {{{20}^2} + {{12}^2}}  = \sqrt {400 + 144}  = \sqrt {544} \)

 \(AB = \sqrt {A{D^2} - B{D^2}}  = \sqrt {{{25}^2} - 544}\) \(  = \sqrt {81}  = 9\)

Vậy ta được kết quả ở bảng sau: 

 

HocTot.Nam.Name.Vn